《2025年课堂点睛八年级数学下册人教版安徽专版》

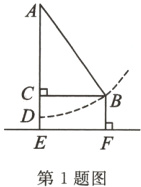
1.(数学与生活)如图是一架秋千的示意图，当它静止时，踏板离地的垂直高度DE = 0.5m，将它往前推送3m(水平距离BC = 3m)时，秋千的踏板离地的垂直高度BF = 1.5m，秋千的绳索始终拉得很直，则绳索AD的长度为____m.

答案： 5

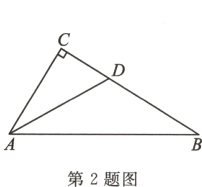
2.如图，在△ABC中，∠C = 90°，AD平分∠CAB交CB于点D，CD = 3，BD = 5，则AD的长为____.

答案： $3\sqrt{5}$

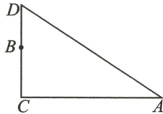
3.如图，在一棵树的10m高的B处有两只猴子，其中一只猴子爬下树，走到离树20m处的池塘A处，另一只猴子爬到树顶D后直接跃向池塘A处(假设它经过的路线为直线)，如果两只猴子所经过的路程相等，求这棵树的高.

答案： 解:设 $BD = xm$,由题意知 $BC + AC = BD + AD$,$\therefore AD=(30 - x)m$,在 $Rt\triangle ACD$ 中,由勾股定理,得 $(10 + x)^{2}+20^{2}=(30 - x)^{2}$,解得 $x = 5$,$\therefore x + 10 = 15$,即这棵树高 15m.

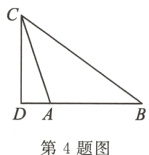
4.如图所示，在△ABC中，AB = AC = 5，BC = 8，CD是AB边上的高，则线段AD的长度为____.

答案： $\frac{7}{5}$

5.如图，在△ABC中，AB = 15，AC = 13，BC = 14，则△ABC的面积为____.

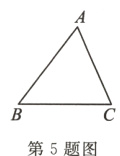
答案： 84

6.(湖南省中考改编)铁路上A，B两站(视为直线上两点)相距25km，C，D为两村庄(视为两个点)，DA⊥AB于点A，CB⊥AB于点B，如图所示，已知DA = 15km，CB = 10km.现在要在铁路AB上建一个土特产收购站E，使得C，D两村庄到收购站E的距离相等，则收购站E应建在距A站____km处.

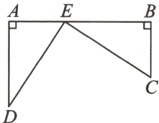
答案： 10

7.如图所示，已知等腰三角形ABC的底边BC = 20cm，D是腰AB上一点，且CD = 16cm，BD = 12cm，求△ABC的周长.

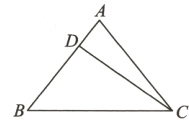
答案： 解:在 $\triangle BCD$ 中,$\because BD^{2}+DC^{2}=12^{2}+16^{2}=400$,$BC^{2}=20^{2}=400$,$\therefore BD^{2}+DC^{2}=BC^{2}$,$\therefore \triangle BCD$ 是直角三角形,且 $\angle BDC = 90^{\circ}$,$\therefore \angle ADC = 180^{\circ}-\angle BDC = 90^{\circ}$. 在 $Rt\triangle ADC$ 中,设 $AD = xcm$,则 $AC = AB=(x + 12)cm$. $\therefore x^{2}+16^{2}=(x + 12)^{2}$,$\therefore x=\frac{14}{3}$,$\therefore C_{\triangle ABC}=(\frac{14}{3}+12)\times2 + 20=\frac{160}{3}(cm)$.