《2025年课堂点睛八年级数学下册人教版安徽专版》

10. 如图，平行四边形ABCD的对角线AC，BD交于点O，AC⊥AB，AB = 2，且AC∶BD = 2∶3.
（1）求AC的长；
（2）求△AOD的面积.

答案：
(1)解：设AC = 2x，则BD = 3x，
∵四边形ABCD是平行四边形，
∴OA = $\frac{1}{2}$AC = x，OB = $\frac{1}{2}$BD = $\frac{3}{2}$x，由OA² + AB² = OB²，得x² + 2² = ( $\frac{3}{2}$x)²，解得x = ± $\frac{4\sqrt{5}}{5}$.
∵x ＞ 0，
∴x = $\frac{4\sqrt{5}}{5}$，
∴AC = $\frac{8\sqrt{5}}{5}$.
(2)S△AOD = S△AOB = $\frac{1}{2}$×2× $\frac{4\sqrt{5}}{5}$ = $\frac{4\sqrt{5}}{5}$.

11.（核心素养·应用意识）如图①，在□ABCD中，对角线AC，BD相交于点O，过点O作直线EF，分别交BC，AD于点E，F.
（1）求证：OF = OE；
（2）小明从图①找到了一种将平行四边形面积平分的方法，你能说说是什么方法吗？

（3）图②是一张纸片，其形状是一个大的平行四边形在一角剪去一个小的平行四边形. 小明发现可以用一条直线将其分割成面积相等的两部分，请你帮助小明设计三种不同的分割方案.

答案：

(1)证明：
∵四边形ABCD是平行四边形，
∴AO = CO，AD//BC，
∴∠FAO = ∠ECO. 在△AOF和△COE中，$\begin{cases} \angle FAO=\angle ECO, \\ AO = CO, \\ \angle AOF=\angle COE, \end{cases}$
∴△AOF≌△COE(ASA).
∴OF = OE.
(2)解：过平行四边形的对角线交点的任意一条直线都能平分其面积.
(3)解：如图所

12. 如图，点E在□ABCD的边AD上，若□ABCD的面积为6，则图中阴影部分的面积为______．

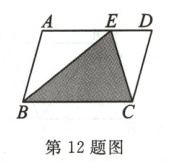
答案： 3

13. 如图，在□ABCD中，AC，BD为对角线，BC = 6，BC边上的高为4，则阴影部分的面积为______．

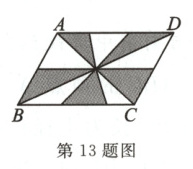
答案： 12

14. 如图，点P是□ABCD内一点，且S△PAB = 7，S△PAD = 4，则阴影部分的面积是______．

答案： 3