第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
8.(河北省中考)如图1,□ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( )
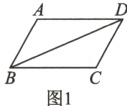
取BD中点U,作AN⊥BD于点N;作CM⊥BD于点M;分别平分∠BAD,∠BCD;BN=NO;OM=MD
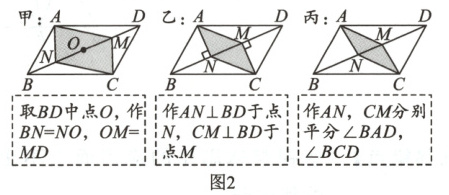
A.甲、乙、丙都是
B.只有甲、乙才是
C.只有甲、丙才是
D.只有乙、丙才是

取BD中点U,作AN⊥BD于点N;作CM⊥BD于点M;分别平分∠BAD,∠BCD;BN=NO;OM=MD

A.甲、乙、丙都是
B.只有甲、乙才是
C.只有甲、丙才是
D.只有乙、丙才是
答案:
A
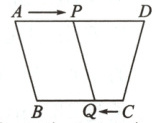
9.如图,在四边形ABCD中,AD//BC,AD = 12 cm,BC =8 cm,P,Q分别从A,C同时出发,P以2 cm/s的速度由A向D运动,Q以1 cm/s的速度由C向B运动,______秒时四边形ABQP是平行四边形.

答案:
$\frac{8}{3}$
10.如图,已知点E,F在四边形ABCD的对角线BD所在的直线上.且BE=DF,AE//CF,请再添加一个条件(不要在图中再增加其他线段和字母),使四边形ABCD是平行四边形,并写出证明过程.
你所添加的条件是_________________.

你所添加的条件是_________________.

答案:
AE = CF(答案不唯一) 证明如下:
∵AE//CF,
∴∠E = ∠F. 又
∵BE = DF,AE = CF,
∴△ABE≌△CDF(SAS).
∴AB = CD,∠ABE = ∠CDF.
∴∠ABD = ∠CDB.
∴AB//CD.
∴四边形ABCD是平行四边形.
∵AE//CF,
∴∠E = ∠F. 又
∵BE = DF,AE = CF,
∴△ABE≌△CDF(SAS).
∴AB = CD,∠ABE = ∠CDF.
∴∠ABD = ∠CDB.
∴AB//CD.
∴四边形ABCD是平行四边形.
11.如图,AM是△ABC的中线,D是线段AM上的一点(不与点A重合),过点D作DE//AB,交过点C且与AM平行的直线于点E,连接AE.
(1)如图①,当点D与点M重合时,求证:四边形ABDE是平行四边形;
(2)如图②,当点D不与点M重合时,(1)中的结论还成立吗?请说明理由.

(1)如图①,当点D与点M重合时,求证:四边形ABDE是平行四边形;
(2)如图②,当点D不与点M重合时,(1)中的结论还成立吗?请说明理由.

答案:
(1)证明:
∵DE//AB,CE//AM,
∴∠EDC = ∠B,∠ECD = ∠AMB. 又
∵AM是△ABC的中线,且点D与点M重合,
∴BD = DC,
∴△ABD≌△EDC(ASA),
∴AB = ED. 又
∵AB//ED,
∴四边形ABDE是平行四边形.
(2)解:成立,理由如下:过点M作MG//DE交CE于点G,
∵MG//DE,DM//CE,
∴四边形DMGE是平行四边形,
∴DE = MG.
∵AB//MG,AM//EC,
∴∠ABC = ∠GMC,∠AMB = ∠GCM. 又
∵AM是△ABC的中线,
∴BM = MC,
∴△ABM≌△GMC(ASA),
∴AB = MG = DE. 又
∵AB//DE,
∴四边形ABDE是平行四边形.
(1)证明:
∵DE//AB,CE//AM,
∴∠EDC = ∠B,∠ECD = ∠AMB. 又
∵AM是△ABC的中线,且点D与点M重合,
∴BD = DC,
∴△ABD≌△EDC(ASA),
∴AB = ED. 又
∵AB//ED,
∴四边形ABDE是平行四边形.
(2)解:成立,理由如下:过点M作MG//DE交CE于点G,
∵MG//DE,DM//CE,
∴四边形DMGE是平行四边形,
∴DE = MG.
∵AB//MG,AM//EC,
∴∠ABC = ∠GMC,∠AMB = ∠GCM. 又
∵AM是△ABC的中线,
∴BM = MC,
∴△ABM≌△GMC(ASA),
∴AB = MG = DE. 又
∵AB//DE,
∴四边形ABDE是平行四边形.
查看更多完整答案,请扫码查看


