第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1.(日照市中考)已知直角三角形的三边a,b,c满足c>a>b,分别以a,b,c为边作三个正方形,把两个较小的正方形放置在最大正方形内,如图,设三个正方形无重叠部分的面积为S₁,均重叠部分的面积为S₂,则 ( )

A. S₁>S₂
B. S₁<S₂
C. S₁=S₂
D. S₁,S₂大小无法确定

A. S₁>S₂
B. S₁<S₂
C. S₁=S₂
D. S₁,S₂大小无法确定
答案:
C
2.(常德市中考)如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若CD=3,BD=5,则BE的长为______.
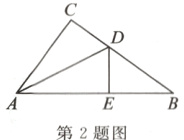

答案:
4
3. 如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,AC=BC=BD=1,若以点A为圆心,AD的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为__________.
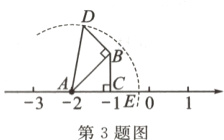

答案:
$-2+\sqrt{3}$
4.(金华市中考)如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2cm.把△ABC沿AB方向平移1cm,得到△A′B′C′,连接CC′,则四边形AB′C′C的周长为__________cm.


答案:
$(8 + 2\sqrt{3})$
5. 下列命题的逆命题是真命题的是 ( )
A. 能被4整除的数一定能被2整除
B. 对顶角相等
C. 全等三角形的对应角相等
D. 两直线平行,内错角相等
A. 能被4整除的数一定能被2整除
B. 对顶角相等
C. 全等三角形的对应角相等
D. 两直线平行,内错角相等
答案:
D
6. “同角的余角相等”的逆命题是____________________.
答案:
如果两个角相等,那么它们是同一个角的余角
7. 三角形的三边a,b,c满足(a+b)²-c²=2ab,则此三角形是 ( )
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 等边三角形
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 等边三角形
答案:
B
8. 五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是 ( )


答案:
C
9. 如图,△ABC中,AC=5,BC=12,AB=13,以AB为直径的半圆过点C,再分别以BC,AC为直径作半圆,则阴影部分面积为__________.
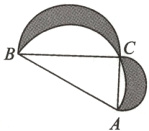

答案:
30
10. 如图,网格中每个小正方形的边长均为1,△ABC的顶点都在格点上.
(1)AB=________,BC=√5,AC=______;
(2)判断△ABC的形状,并说明理由.
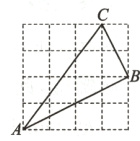
(1)AB=________,BC=√5,AC=______;
(2)判断△ABC的形状,并说明理由.

答案:
(1)$2\sqrt{5}$,5
(2)解:$\triangle ABC$是直角三角形. 理由如下:$\because AB = 2\sqrt{5},BC=\sqrt{5},AC = 5,\therefore AB^{2}+BC^{2}=(2\sqrt{5})^{2}+(\sqrt{5})^{2}=20 + 5 = 25 = AC^{2},\therefore \triangle ABC$是直角三角形.
(1)$2\sqrt{5}$,5
(2)解:$\triangle ABC$是直角三角形. 理由如下:$\because AB = 2\sqrt{5},BC=\sqrt{5},AC = 5,\therefore AB^{2}+BC^{2}=(2\sqrt{5})^{2}+(\sqrt{5})^{2}=20 + 5 = 25 = AC^{2},\therefore \triangle ABC$是直角三角形.
查看更多完整答案,请扫码查看


