《2025年课堂点睛八年级数学下册人教版安徽专版》

11.在学习“勾股数”的知识时，爱思考的小琦发现了一组有规律的勾股数，并将它们记录在如下的表格中：

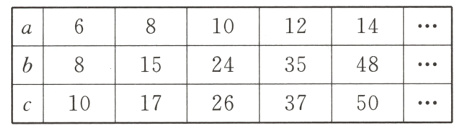
则当a = 18时，b + c的值为（ ）
A.242 B.200 C.128 D.162

答案： D

12.（玉林市中考）如图，某港口P位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行12海里和16海里，1小时后两船分别位于点A，B处，且相距20海里，如果知道甲船沿北偏西40°方向航行，则乙船沿____________方向航行.

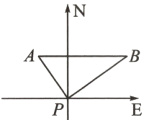
答案： 北偏东50°

13.如图，在Rt△ABC中，∠ACB = 90°，AB = 5cm，AC = 3cm，动点P从点B出发，沿射线BC以2cm/s的速度移动，设运动的时间为t s，则当t = __________时△ABP为直角三角形.

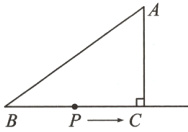
答案： 2或25/8

14.如图，在四边形ABCD中，∠B = 90°，AB = BC = 2，AD = $\sqrt{2}$，CD = $\sqrt{10}$，求∠BAD的度数.

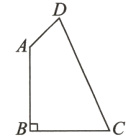
答案： 解:连接AC,
∵∠B = 90°,AB = BC = 2,
∴∠BAC = ∠BCA = 45°,AC = √(AB² + BC²)=√(2² + 2²)=2√2.又
∵AD = √2,CD = √10,
∴AD² + AC² = CD²,
∴△ACD是直角三角形，且∠DAC = 90°,
∴∠DAB = ∠DAC + ∠BAC = 90° + 45° = 135°.

15.如图所示，甲、乙两船从港口A同时出发，甲船以30海里/时的速度向北偏东35°的方向航行，乙船以40海里/时的速度向另一方向航行，2小时后，甲船到达C岛，乙船到达B岛，若C，B两岛相距100海里，则乙船航行的角度是南偏东多少度？

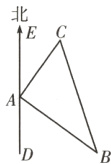
答案： 解:由题意，可知AC = 60海里,AB = 80海里，BC = 100海里，
∵AC² + AB² = BC²,
∴∠CAB = 90°,
∴∠DAB = 180° - ∠CAB - ∠CAE = 55°,
∴乙船航行的角度为南偏东55°.

16.（核心素养·创新意识）张老师在一次“探究性学习”中设计了下表：

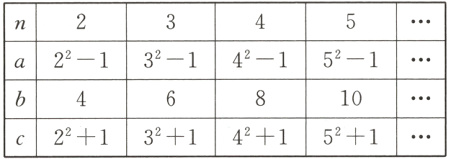
（1）请你分别观察a，b，c与n之间的关系，并用含n（n＞1，且是自然数）的式子表示a，b，c.
a = ______，b = ______，c = ______；
（2）猜想以a，b，c为边长的三角形是不是直角三角形，并证明你的猜想.

答案：
(1)n² - 1 2n n² + 1
(2)解:是直角三角形.证明如下:
∵a = n² - 1,b = 2n,c = n² + 1,
∴a² + b² = (n² - 1)² + (2n)² = (n² + 1)²,c² = (n² + 1)².
∴a² + b² = c²,
∴以a,b,c为边长的三角形是直角三角形.