《2025年课堂点睛八年级数学下册人教版安徽专版》

8.如图，已知正方形ABCD的边长为1，连接AC,BD交于点O，CE平分∠ACD交BD于点E，则DE = __________.
　　　　　　　　　　　

答案： $\sqrt{2}$ - 1

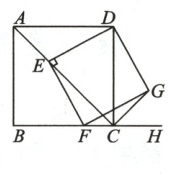
9.（核心素养·推理能力）如图，点E为边长为2的正方形ABCD的对角线AC上的一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE,EF为邻边作矩形DEFG，连接CG.
　(1)求证:矩形DEFG是正方形;
　(2)探究:CE十CG的值是否为定值？若是，请求出这个定值;若不是，请说明理由.

答案：
(1)证明:过点E分别作EM⊥BC于点M，EN⊥CD于点N，则∠EMC = ∠ENC = ∠END = 90°.又
∵四边形ABCD是正方形，
∴∠BCD = 90°，∠ACB = ∠ACD = 45°，
∴∠MEN = 90°，EM = EN.又
∵EF⊥DE，
∴∠DEF = 90° = ∠MEN，
∴∠DEN = ∠FEM，又EF = DE，
∴△DEN≌△FEM，
∴矩形DEFG是正方形.
(2)解:CE + CG的值为定值$2\sqrt{2}$，理由如下：
∵四边形DEFG和四边形ABCD都是正方形，
∴AD = DC，DE = DG，∠ADC = ∠EDG = 90°，
∴∠ADE = ∠CDG，
∴△ADE≌△CDG，
∴AE = CG，
∴CE + CG = CE + AE = AC = $\sqrt{AB^{2}+BC^{2}}$ = $\sqrt{2^{2}+2^{2}}$ = $2\sqrt{2}$，
∴CE + CG的值是定值$2\sqrt{2}$.

10.[变式1]已知:如图，在正方形ABCD中，对角线AC,BD相交于点O，点E,F分别是边BC,CD上的点，且∠EOF = 90°.求证:CE = DF.
　　　　　　　　　　　　　

答案： 证明:
∵四边形ABCD为正方形，
∴OD = OC，∠ODF = ∠OCE = 45°，∠COD = 90°，
∴∠DOF + ∠COF = 90°.
∵∠EOF = 90°，即∠COE + ∠COF = 90°，
∴∠COE = ∠DOF.
∴△COE≌△DOF(ASA).
∴CE = DF.

11.[变式2]如图，△ABC是等腰直角三角形，∠BAC = 90°，点P,Q分别是AB,AC 上的动点，且满足BP = AQ，D是BC的中点.
　　(1)求证:△PDQ是等腰直角三角形;
　　(2)当P运动到什么位置时，四边形AP - DQ是正方形？并说明理由.
　　　　　　　　　　

答案：
(1)证明:连接AD.
∵△ABC是等腰直角三角形，D是BC的中点，
∴AD⊥BC，AD = BD = DC，∠DAQ = ∠B.又
∵BP = AQ，
∴△BPD≌△AQD.
∴PD = QD，∠ADQ = ∠BDP.
∵∠BDP + ∠ADP = 90°，
∴∠ADQ + ∠ADP = ∠PDQ = 90°，
∴△PDQ为等腰直角三角形.
(2)当P运动到AB的中点时，四边形APDQ为正方形.理由:由
(1)知△ABD为等腰直角三角形.当P为AB的中点时，DP⊥AB，即∠APD = 90°.又
∵∠BAC = 90°，∠PDQ = 90°，
∴四边形APDQ为矩形.又
∵DP = AP = $\frac{1}{2}$AB，
∴四边形APDQ为正方形.