第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
8.(教材第68页第9题变式)如图,顺次连接四边形ABCD各边的中点,得到四边形EFGH.在下列条件中,可使四边形EFGH为矩形的是( )
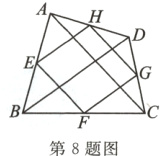
A. AB = CD
B. AC = BD
C. AC⊥BD
D. AD//BC

A. AB = CD
B. AC = BD
C. AC⊥BD
D. AD//BC
答案:
C
9.如图,点M是矩形ABCD的边AD的中点,P是BC上一点,PE⊥MC,PF⊥MB,当AB,BC满足条件____________________时,四边形PEMF为矩形.


答案:
BC = 2AB
10.(泰州市中考)如图,线段DE与AF分别为△ABC的中位线与中线.
(1)求证:AF与DE互相平分;
(2)当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形?请说明理由.

(1)求证:AF与DE互相平分;
(2)当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形?请说明理由.

答案:
(1)证明:
∵线段DE与AF分别为△ABC的中位线与中线,
∴AD = BD = $\frac{1}{2}$AB,AE = CE,BF = CF,
∴EF是△ABC的中位线,
∴EF//AB,EF = $\frac{1}{2}$AB,
∴EF = AD,
∴四边形ADFE是平行四边形,
∴AF与DE互相平分.
(2)解:当AF = $\frac{1}{2}$BC时,四边形ADFE为矩形,理由如下:
∵线段DE为△ABC的中位线,
∴DE = $\frac{1}{2}$BC. 又
∵AF = $\frac{1}{2}$BC,
∴AF = DE.
∵四边形ADFE是平行四边形,
∴四边形ADFE为矩形.
(1)证明:
∵线段DE与AF分别为△ABC的中位线与中线,
∴AD = BD = $\frac{1}{2}$AB,AE = CE,BF = CF,
∴EF是△ABC的中位线,
∴EF//AB,EF = $\frac{1}{2}$AB,
∴EF = AD,
∴四边形ADFE是平行四边形,
∴AF与DE互相平分.
(2)解:当AF = $\frac{1}{2}$BC时,四边形ADFE为矩形,理由如下:
∵线段DE为△ABC的中位线,
∴DE = $\frac{1}{2}$BC. 又
∵AF = $\frac{1}{2}$BC,
∴AF = DE.
∵四边形ADFE是平行四边形,
∴四边形ADFE为矩形.
11.(核心素养·推理能力)如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,连接BE并延长与CD的延长线交于点F,连接AF,∠BDF = 90°.
(1)求证:四边形ABDF是矩形;
(2)若AD = 5,DF = 3,求四边形ABCF的面积S.
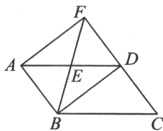
(1)求证:四边形ABDF是矩形;
(2)若AD = 5,DF = 3,求四边形ABCF的面积S.

答案:
(1)证明:
∵四边形ABCD是平行四边形,
∴AB//CD,
∴AB//DF.
∴∠DFE = ∠ABE.
∵E为线段AD的中点,
∴DE = AE. 在△DFE和△ABE中,$\begin{cases}∠DFE = ∠ABE,\\∠DEF = ∠AEB,\\DE = AE,\end{cases}$
∴△DFE≌△ABE(AAS).
∴DF = AB. 又
∵AB//DF,
∴四边形ABDF是平行四边形.
∵∠BDF = 90°,
∴平行四边形ABDF是矩形.
(2)解:
∵四边形ABDF是矩形,
∴∠AFD = 90°,AF = BD,AB = DF.
∵AD = 5,DF = 3.
∴在Rt△AFD中,AF = $\sqrt{AD^{2}-DF^{2}}=\sqrt{5^{2}-3^{2}} = 4$.
∴BD = AF = 4,AB = DF = 3.
∵四边形ABCD是平行四边形,
∴CD = AB = 3.
∴S_{四边形ABCF}=S_{矩形ABDF}+S_{△BCD}=DF·BD+$\frac{1}{2}$CD·BD = 3×4+$\frac{1}{2}$×3×4 = 18.
(1)证明:
∵四边形ABCD是平行四边形,
∴AB//CD,
∴AB//DF.
∴∠DFE = ∠ABE.
∵E为线段AD的中点,
∴DE = AE. 在△DFE和△ABE中,$\begin{cases}∠DFE = ∠ABE,\\∠DEF = ∠AEB,\\DE = AE,\end{cases}$
∴△DFE≌△ABE(AAS).
∴DF = AB. 又
∵AB//DF,
∴四边形ABDF是平行四边形.
∵∠BDF = 90°,
∴平行四边形ABDF是矩形.
(2)解:
∵四边形ABDF是矩形,
∴∠AFD = 90°,AF = BD,AB = DF.
∵AD = 5,DF = 3.
∴在Rt△AFD中,AF = $\sqrt{AD^{2}-DF^{2}}=\sqrt{5^{2}-3^{2}} = 4$.
∴BD = AF = 4,AB = DF = 3.
∵四边形ABCD是平行四边形,
∴CD = AB = 3.
∴S_{四边形ABCF}=S_{矩形ABDF}+S_{△BCD}=DF·BD+$\frac{1}{2}$CD·BD = 3×4+$\frac{1}{2}$×3×4 = 18.
查看更多完整答案,请扫码查看


