《2025年课堂点睛八年级数学下册人教版安徽专版》

11.（数学与生活）某市出租车白天的收费起步价为14元，即路程不超过3千米时收费14元，超过部分每千米收费2.4元.如果乘客白天乘坐出租车的路程为$x(x＞3)$千米，乘车费为$y$元，那么$y$与$x$之间的关系式为____________.

答案： $y = 2.4x + 6.8$

12.已知$y + 2$与$x$成正比例，且当$x = 6$时，$y = 1$.
（1）求这个函数的解析式，并指出$y$是$x$的什么函数？
（2）当$x$的值从 - 3增大到3时，函数值$y$是如何变化的？

答案：
(1)解：设$y + 2 = kx,\therefore1 + 2 = 6k,k=\frac{1}{2},\therefore y=\frac{1}{2}x - 2$，$y$是$x$的一次函数.
(2)当$x = -3$时，$y=\frac{-3}{2}-2=-\frac{7}{2}$；当$x = 3$时，$y=\frac{3}{2}-2=-\frac{1}{2}$.即函数值$y$从$-\frac{7}{2}$增大到$-\frac{1}{2}$.

13.（长沙市中考改编）如图，在$\triangle ABC$中，$\angle ABC$与$\angle ACB$的平分线交于点$P$，设$\angle A = x$，$\angle BPC = y$，当$\angle A$变化时，求$y$与$x$之间的函数关系式，并判断$y$是不是$x$的一次函数，指出自变量的取值范围.

答案： 解：在$\triangle ABC$中，$\because\angle A = x$，$BP,CP$分别是$\angle ABC$与$\angle ACB$的平分线，$\therefore\angle PBC+\angle PCB=\frac{180^{\circ}-x}{2}$. 在$\triangle BPC$中，$\angle BPC = 180^{\circ}-(\angle PBC+\angle PCB)$，$\therefore y = 180^{\circ}-\frac{180^{\circ}-x}{2}$，即$y = 90^{\circ}+\frac{1}{2}x$. $\therefore y$是$x$的一次函数，$x$的取值范围是$0^{\circ}＜x＜180^{\circ}$.

14.（核心素养·应用意识）李叔叔批发甲、乙两种蔬菜到菜市场去卖，已知甲、乙两种蔬菜的批发价和零售价如下表所示：

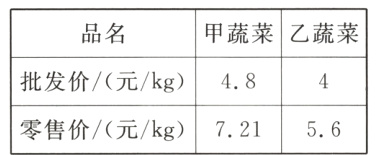
（1）若他批发甲、乙两种蔬菜共80kg，花费$m$元，设批发甲种蔬菜$n$kg，则$m$与$n$的函数关系式为____________；
（2）在（1）的条件下，全部蔬菜卖完后要保证利润不低于168.5元，至少批发甲种蔬菜多少千克？

答案：
(1)$m = 0.8n + 320$
(2)解：设全部蔬菜卖完后利润为$w$元，根据题意得$w=(7.21 - 4.8)n+(5.6 - 4)(80 - n)$，整理得$w = 0.81n + 128$. $\because$要保证利润不低于168.5元，$\therefore w = 0.81n + 128\geqslant168.5$，解得$n\geqslant50$. $\therefore$至少批发甲种蔬菜50kg.