《2025年课堂点睛八年级数学下册人教版安徽专版》

1.在△ABC中，∠A，∠B，∠C的对边分别是a，b，c.若∠B = 90°，则下列等式中成立的是（ ）
A.a² + b² = c²
B.b² + c² = a²
C.a² + c² = b²
D.c² - a² = b²

答案： C

2.（成都市中考）如图，数字代表所在正方形的面积，则A所代表的正方形的面积为______.

答案： 100

3.（探索与验证）如图是由边长均为1的正方形组成的网格，下面是勾股定理的探索与验证过程，请补充完整：
∵S₁ = ______，S₂ = ______，S₃ = ______，
∴S₁ + S₂ = S₃.
即______² + ______² = ______².

答案： 4 9 13 AC BC AB

4.以a，b为直角边，以c为斜边作全等的直角三角形△ACE和△BDE，把这两个直角三角形拼成如图所示形状，使A，E，B三点在一条直线上.求证：a² + b² = c².

答案： 证明:易证∠CED = 90°.由图可得$\frac{1}{2}(a + b)\cdot(a + b)=\frac{1}{2}ab+\frac{1}{2}c^{2}+\frac{1}{2}ab$,整理得$\frac{a^{2}+2ab + b^{2}}{2}=\frac{2ab + c^{2}}{2}$,则$a^{2}+2ab + b^{2}=2ab + c^{2}$,故$a^{2}+b^{2}=c^{2}$.

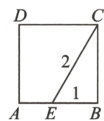
5.如图，点E在正方形ABCD的边AB上，若EB = 1，EC = 2，则正方形ABCD的面积为（ ）

A.√3
B.3
C.√5
D.5

答案： B

6.（临沂市中考）如图，每个小正方形的边长都为1，点A，B都在格点上，若BC = 2√13/3，则AC的长为__________.

答案： $\frac{4\sqrt{13}}{3}$

7.（原创题）平面直角坐标系中，点P（-4，3）到原点的距离是______.

答案： 5

8.如图，在Rt△ABC中，∠C = 90°，∠A，∠B，∠C的对边长分别是a，b，c.
（1）若a = 3，b = 2√3，求c的值；
（2）若b = 4，c = 8，求a的值；
（3）若a : c = 3 : 5，b = 32，求a，c的值.

答案： 解:
(1)$c=\sqrt{a^{2}+b^{2}}=\sqrt{3^{2}+(2\sqrt{3})^{2}}=\sqrt{21}$.
(2)$a=\sqrt{c^{2}-b^{2}}=\sqrt{8^{2}-4^{2}}=4\sqrt{3}$.
(3)设$a = 3x,c = 5x,\because a^{2}+b^{2}=c^{2},\therefore(3x)^{2}+32^{2}=(5x)^{2}$,解得$x = 8$,(负值已舍去)$\therefore a = 3x = 24,c = 5x = 40$.