第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
10. 有一根长为7cm的木棒,要将其放进长、宽、高分别为5cm,4cm,3cm的长方体木箱中,______(填“能”或“不能”)放进去.
答案:
能
11.(武汉市中考)如图,沿AB方向架桥修路,为加快施工进度,在直线AB上湖的另一边的D处同时施工. 取∠ABC = 150°,BC = 1600m,∠BCD = 105°,则C,D两点的距离是__________m.
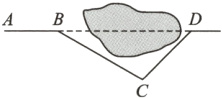

答案:
$800\sqrt{2}$
12. 如图①②是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长都是1,请在方格纸中分别画出符合下列要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个面积为5的等腰直角三角形;
(2)画一个三边长分别为3,2$\sqrt{2}$,$\sqrt{5}$的三角形.
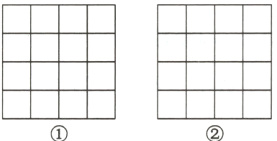
(1)画一个面积为5的等腰直角三角形;
(2)画一个三边长分别为3,2$\sqrt{2}$,$\sqrt{5}$的三角形.

答案:
解:
(1)如图① ,直角边为$\sqrt{10}$的等腰直角三角形即为所求.
,直角边为$\sqrt{10}$的等腰直角三角形即为所求.
(2)如图② ,三边分别为$3,2\sqrt{2},\sqrt{5}$的三角形即为所求.(画法均不唯一)
,三边分别为$3,2\sqrt{2},\sqrt{5}$的三角形即为所求.(画法均不唯一)
解:
(1)如图①
 ,直角边为$\sqrt{10}$的等腰直角三角形即为所求.
,直角边为$\sqrt{10}$的等腰直角三角形即为所求.(2)如图②
 ,三边分别为$3,2\sqrt{2},\sqrt{5}$的三角形即为所求.(画法均不唯一)
,三边分别为$3,2\sqrt{2},\sqrt{5}$的三角形即为所求.(画法均不唯一) 13.(湖北省中考改编)如图,在长方形ABCD中,AB = 12cm,BC = 24cm,将该长方形沿对角线BD折叠.
(1)判断△BED的形状,并说明理由;
(2)求BE的长.
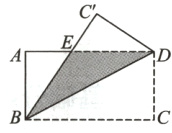
(1)判断△BED的形状,并说明理由;
(2)求BE的长.

答案:
解:
(1)$\triangle BED$为等腰三角形. 理由如下:由题意得$\angle A=\angle C=\angle C' = 90^{\circ}$,$AB = CD = C'D$. 又$\angle AEB=\angle C'ED$,$\therefore \triangle AEB\cong\triangle C'ED(AAS)$.$\therefore BE = DE$.$\therefore \triangle BED$为等腰三角形.
(2)由题意得$AD = BC = 24$cm. 设$BE = DE = x$cm,则$AE = AD - DE=(24 - x)$cm. 在$Rt\triangle ABE$中,由勾股定理,得$BE^{2}=AB^{2}+AE^{2}$,即$x^{2}=12^{2}+(24 - x)^{2}$,解得$x = 15$.$\therefore BE$的长为15 cm.
(1)$\triangle BED$为等腰三角形. 理由如下:由题意得$\angle A=\angle C=\angle C' = 90^{\circ}$,$AB = CD = C'D$. 又$\angle AEB=\angle C'ED$,$\therefore \triangle AEB\cong\triangle C'ED(AAS)$.$\therefore BE = DE$.$\therefore \triangle BED$为等腰三角形.
(2)由题意得$AD = BC = 24$cm. 设$BE = DE = x$cm,则$AE = AD - DE=(24 - x)$cm. 在$Rt\triangle ABE$中,由勾股定理,得$BE^{2}=AB^{2}+AE^{2}$,即$x^{2}=12^{2}+(24 - x)^{2}$,解得$x = 15$.$\therefore BE$的长为15 cm.
14.(核心素养·模型观念)如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风的影响有多长时间?
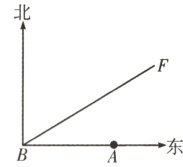
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风的影响有多长时间?

答案:
解:
(1)$A$城会受到这次台风影响,理由如下:如图 ,过点$A$作$AC\perp BF$于$C$. 在$Rt\triangle ABC$中,$\angle ABC = 30^{\circ}$,$AB = 320$km,$\therefore AC = 160$km$< 200$km,$\therefore A$城会受到台风的影响.
,过点$A$作$AC\perp BF$于$C$. 在$Rt\triangle ABC$中,$\angle ABC = 30^{\circ}$,$AB = 320$km,$\therefore AC = 160$km$< 200$km,$\therefore A$城会受到台风的影响.
(2)$\because AC = 160$km$< 200$km,$\therefore$在$BF$上存在点$G$和点$D$满足$AD = AG = 200$km(如图).$\because AD = AG$,$AC\perp BF$,$\therefore DG = 2CD = 2\sqrt{200^{2}-160^{2}} = 240$(km),$\therefore t = 240\div40 = 6$(h). $\therefore A$城遭受这次台风的影响有6 h.
解:
(1)$A$城会受到这次台风影响,理由如下:如图
 ,过点$A$作$AC\perp BF$于$C$. 在$Rt\triangle ABC$中,$\angle ABC = 30^{\circ}$,$AB = 320$km,$\therefore AC = 160$km$< 200$km,$\therefore A$城会受到台风的影响.
,过点$A$作$AC\perp BF$于$C$. 在$Rt\triangle ABC$中,$\angle ABC = 30^{\circ}$,$AB = 320$km,$\therefore AC = 160$km$< 200$km,$\therefore A$城会受到台风的影响. (2)$\because AC = 160$km$< 200$km,$\therefore$在$BF$上存在点$G$和点$D$满足$AD = AG = 200$km(如图).$\because AD = AG$,$AC\perp BF$,$\therefore DG = 2CD = 2\sqrt{200^{2}-160^{2}} = 240$(km),$\therefore t = 240\div40 = 6$(h). $\therefore A$城遭受这次台风的影响有6 h.
查看更多完整答案,请扫码查看


