《2025年课堂点睛八年级数学下册人教版安徽专版》

9.已知直角三角形的两边长分别为3和4，则第三边的长为（ ）
A.5
B.7
C.√5
D.5或√7

答案： D

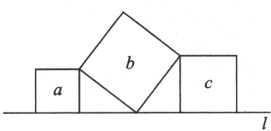
10.（教材第24页第2题变式）如图，直线l上有三个正方形a，b，c，若a，c的面积分别为3和4，则b的面积为（ ）

A.3
B.4
C.5
D.7

答案： D

11.如图，在Rt△ABC中，∠ACB = 90°，AB = 4，分别以AC，BC为直径作半圆，面积分别记为S₁，S₂，则S₁ + S₂的值等于______.

答案： 2π

12.如图，在△ABC中，∠B = 45°，∠C = 30°，AB = √6.
（1）求边AC的长；
（2）求△ABC的面积.

答案： 解:
(1)过点A作AD⊥BC于D,则∠BDA = ∠ADC = 90°,
∵∠B = 45°,∠C = 30°,
∴∠BAD = 45°,AD = $\frac{1}{2}$AC,
∴∠B = ∠BAD,
∴BD = AD,在Rt△ABD中,$2AD^{2}=AB^{2}$,
∴$AD=\sqrt{3}$,
∴$AC = 2\sqrt{3}$.
(2)在Rt△ACD中,$CD=\sqrt{AC^{2}-AD^{2}} = 3$.
∴$BC = BD + CD=\sqrt{3}+3$,
∴$S_{\triangle ABC}=\frac{1}{2}\cdot BC\cdot AD=\frac{1}{2}\times(\sqrt{3}+3)\times\sqrt{3}=\frac{3}{2}+\frac{3}{2}\sqrt{3}$.

13.（一题多变）以直角三角形的三边为边向外作正方形，如图①所示，三个正方形的面积分别为S₁，S₂，S₃，则有S₁ + S₂ ______ S₃（填“＞”“＝”或“＜”）.

答案： =

【变式1】分别以直角三角形的三边为直径向外作半圆，如图②所示，上述结论是否仍成立？说明理由.

答案： 成立.理由如下:
∵$S_{1}=\frac{\pi}{8}\cdot b^{2},S_{2}=\frac{\pi}{8}\cdot a^{2},S_{3}=\frac{\pi}{8}\cdot c^{2},a^{2}+b^{2}=c^{2}$,
∴$S_{1}+S_{2}=S_{3}$.即上述结论仍然成立.

【变式2】如图③，以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB = √3，则图中阴影部分的面积为__________.

答案： 3

【变式3】如图④，分别以Rt△ABC的三边为边向外作等边三角形.若AB = 4，则S₁ + S₂ = ________.

答案： $4\sqrt{3}$