《2025年课堂点睛八年级数学下册人教版安徽专版》

1.(河南省中考)关于菱形的性质，以下说法不正确的是（ ）
A. 四条边相等
B. 对角线相等
C. 对角线互相垂直
D. 是轴对称图形

答案： B

2.(黔东南州中考)如图，BD是菱形ABCD的一条对角线，点E在BC的延长线上.若∠ADB=32°，则∠DCE的度数为______.

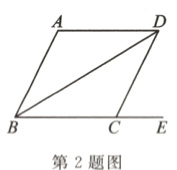
答案： $64^{\circ}$

3.(长沙市中考改编)如图，菱形ABCD的对角线AC，BD相交于点O，E是边AB的中点，若OE=6，则BC的长为______.

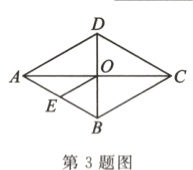
答案： 12

4.(达州市中考)如图，菱形ABCD的对角线AC与BD相交于点O，AC=24，BD=10，则菱形ABCD的周长是______.

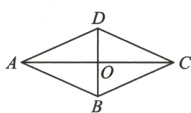
答案： 52

5.(菏泽市中考)如图，在菱形ABCD中，点M，N分别在AB，CB上，且∠ADM=∠CDN. 求证：BM=BN.

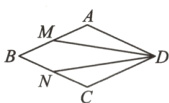
答案： 证明：
∵四边形ABCD是菱形，
∴$AD = CD = AB = BC$，$∠A = ∠C$，又$∠ADM = ∠CDN$，
∴$\triangle AMD\cong\triangle CND(ASA)$．
∴$AM = CN$．
∴$AB - AM = BC - CN$，
∴$BM = BN$．

6.(乐山市中考)已知菱形ABCD的两条对角线AC，BD的长分别是8cm和6cm，则菱形的面积为________.

答案： $24cm^{2}$

7.(教材第56页例3变式)如图，沿着菱形花圃ABCD的对角线修建有两条小路AC和BD，若∠ABC=120°，AC=12m，则花圃的面积为________m².

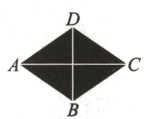
答案： $24\sqrt{3}$

8.如图，两条宽度为1的纸带相交成60°角，重叠部分为菱形，求菱形的面积.

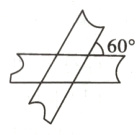
答案：
解：如图 ，设菱形ABCD，则$∠ABE = 60^{\circ}$，过点A作$AE⊥BC$于点E，则AE = 1．设$BE = x$，
∵$∠ABE = 60^{\circ}$，
∴$∠BAE = 30^{\circ}$，
∴$AB = 2x$，$AE=\sqrt{AB^{2}-BE^{2}}=\sqrt{(2x)^{2}-x^{2}}=\sqrt{3}x=1$，
∴$x=\frac{\sqrt{3}}{3}$，
∴$AB = BC = 2x=\frac{2\sqrt{3}}{3}$，
∴重叠部分的面积是$S=BC\cdot AE=\frac{2\sqrt{3}}{3}\times1=\frac{2\sqrt{3}}{3}$．

9.在菱形ABCD中，边长AB=6，∠A=60°，若点P是菱形内一点，且PB=PD=2$\sqrt{3}$，则AP的长是___________.

答案： $2\sqrt{3}$或$4\sqrt{3}$

10.(宁夏自治区中考)如图，菱形ABCD的边长为13，对角线AC=24，点E，F分别是边CD，BC的中点，连接EF并延长与AB的延长线相交于点G，则EG=（ ）

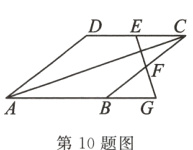
A. 13
B. 10
C. 12
D. 5

答案： B