《2025年课堂点睛八年级数学下册人教版安徽专版》

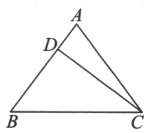
11. 如图，已知等腰三角形ABC的底边BC＝20cm，D是腰AB上一点，且CD＝16cm，BD＝12cm.
（1）求证：CD⊥AB；
（2）求三角形ABC的腰长.

答案：
(1)证明：$\because BC = 20cm,CD = 16cm,BD = 12cm,\therefore BD^{2}+CD^{2}=BC^{2}.\therefore \angle BDC = 90^{\circ}$，即$CD\perp AB$.
(2)解：设三角形$ABC$的腰长为$x cm$，则$AD=(x - 12)cm$. 由勾股定理可知$AD^{2}+CD^{2}=AC^{2}$，即$(x - 12)^{2}+16^{2}=x^{2}$，解得$x=\frac{50}{3}.\therefore$该三角形的腰长为$\frac{50}{3}cm$.

12. 甲、乙两艘轮船同时从港口出发，甲以16海里/时的速度向北偏东75°的方向航行.它们出发1.5小时后，两船相距30海里.若乙以12海里/时的速度航行，则它的航行方向为 （ ）
A. 北偏西15°
B. 南偏西75°
C. 南偏东15或北偏西15°
D. 南偏西15°或北偏东15°

答案： C

13. △ABC中，AC＝3，AB＝4，当BC＝__________时，△ABC是直角三角形.

答案： 5或$\sqrt{7}$

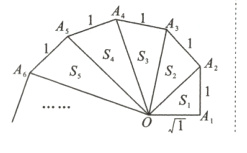
14. 仔细观察图形，认真分析下列各式，然后解答问题.
$OA_{2}^{2}=(\sqrt{1})^{2}+1 = 2,S_{1}=\frac{\sqrt{1}}{2}$；
$OA_{3}^{2}=(\sqrt{2})^{2}+1 = 3,S_{2}=\frac{\sqrt{2}}{2}$；
$OA_{4}^{2}=(\sqrt{3})^{2}+1 = 4,S_{3}=\frac{\sqrt{3}}{2}$；
……
求：
（1）推算出OA₁₀的长；
（2）求出$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots+S_{10}^{2}$的值.

答案：
(1)解：$OA_{10}^{2}=(\sqrt{9})^{2}+1 = 10,\therefore OA_{10}=\sqrt{10}$.
(2)$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots+S_{10}^{2}=(\frac{1}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}+\cdots+(\frac{\sqrt{9}}{2})^{2}+(\frac{\sqrt{10}}{2})^{2}=\frac{1}{4}+\frac{2}{4}+\frac{3}{4}+\cdots+\frac{9}{4}+\frac{10}{4}=\frac{1 + 2+3+\cdots+9 + 10}{4}=\frac{55}{4}$.

15. 通过对《勾股定理》的学习，我们知道：如果一个三角形中，两边的平方和等于第三边的平方，那么这个三角形一定是直角三角形，如果我们新定义一种三角形，两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
（1）根据奇异三角形的定义，请你判断：等边三角形一定是奇异三角形吗？______（填“是”或“不是”）.
（2）若某三角形的三边长分别为1，√7，2，则该三角形是不是奇异三角形？请做出判断并写出判断依据.
（3）在Rt△ABC中，三边长分别为a，b，c，且$a^{2}=50$，$c^{2}=100$，则这个三角形是不是奇异三角形？请做出判断并写出判断依据.
探究：在Rt△ABC中，∠C＝90°，AB＝c，AC＝b，BC＝a，且b＞a. 若Rt△ABC是奇异三角形，求$a^{2}:b^{2}:c^{2}$.
数学·八年级下册 28

答案：
(1)是
(2)解：该三角形是奇异三角形，理由如下：$\because 1^{2}+(\sqrt{7})^{2}=2\times 2^{2},\therefore$该三角形是奇异三角形.
(3)当$c$为斜边时，$b^{2}=c^{2}-a^{2}=50$，$Rt\triangle ABC$不是奇异三角形；当$b$为斜边时，$b^{2}=c^{2}+a^{2}=150,\because 50 + 150 = 2\times 100,\therefore a^{2}+b^{2}=2c^{2}.\therefore Rt\triangle ABC$是奇异三角形.
探究：$Rt\triangle ABC$中，$\angle C = 90^{\circ},\therefore a^{2}+b^{2}=c^{2}.\because c＞b＞a.\therefore 2c^{2}＞b^{2}+a^{2},2a^{2}＜b^{2}+c^{2}.\because Rt\triangle ABC$是奇异三角形，$\therefore 2b^{2}=a^{2}+c^{2}.\therefore 2b^{2}=a^{2}+a^{2}+b^{2}.\therefore b^{2}=2a^{2}.\therefore c^{2}=3a^{2}.\therefore a^{2}:b^{2}:c^{2}=1:2:3$.