第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
12.(核心素养·运算能力)阅读下列解题过程:
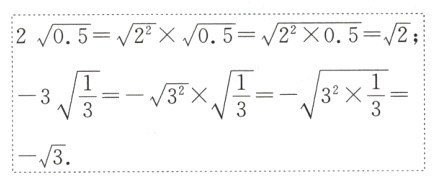
利用上述解法化简下列各式:
(1)$10\sqrt{0.1}$;
(2)$x\sqrt{-\frac{1}{x}}$.
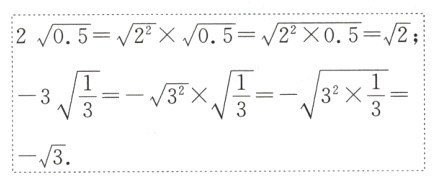
利用上述解法化简下列各式:
(1)$10\sqrt{0.1}$;
(2)$x\sqrt{-\frac{1}{x}}$.
答案:
(1)解:$10\sqrt{0.1}=\sqrt{10^{2}}\times\sqrt{0.1}=\sqrt{100\times0.1}=\sqrt{10}$。
(2)因为$-\frac{1}{x}>0$,所以$x<0$,所以$x\sqrt{-\frac{1}{x}}=-\sqrt{x^{2}}\cdot\sqrt{-\frac{1}{x}}=-\sqrt{x^{2}\cdot(-\frac{1}{x})}=-\sqrt{-x}$。
(1)解:$10\sqrt{0.1}=\sqrt{10^{2}}\times\sqrt{0.1}=\sqrt{100\times0.1}=\sqrt{10}$。
(2)因为$-\frac{1}{x}>0$,所以$x<0$,所以$x\sqrt{-\frac{1}{x}}=-\sqrt{x^{2}}\cdot\sqrt{-\frac{1}{x}}=-\sqrt{x^{2}\cdot(-\frac{1}{x})}=-\sqrt{-x}$。
13.【阅读】古希腊的几何学家海伦,在数学史上以解决几何测量问题而闻名,在他的著作《度量》一书中,给出了一个公式:如果一个三角形的三边长分别为$a$,$b$,$c$,记$p = \frac{a + b + c}{2}$,则三角形的面积$S = \sqrt{p(p - a)(p - b)(p - c)}$,此公式称为“海伦公式”.
【思考运用】
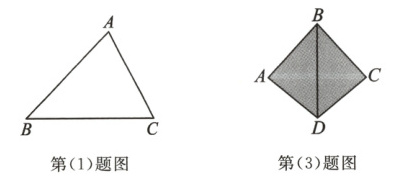
(1)已知李大爷有一块三角形的菜地,如图,测得$AB = 8\text{ m}$,$AC = 7\text{ m}$,$BC = 9\text{ m}$,则李大爷这块菜地的面积为________$\text{m}^2$.
(2)在上面【阅读】材料基础上,若$p = 5\text{cm}$,$a = 3\text{cm}$,$c = 4\text{cm}$,则此三角形的面积为________$\text{cm}^2$.
(3)如图是小明制作的一个风筝模型,其中$AB = BC = 50\text{cm}$,$AD = CD = 40\text{cm}$,$BD = 60\text{cm}$,请你用海伦公式帮助小明求风筝模型$ABCD$的面积为________$\text{cm}^2$.

【思考运用】
(1)已知李大爷有一块三角形的菜地,如图,测得$AB = 8\text{ m}$,$AC = 7\text{ m}$,$BC = 9\text{ m}$,则李大爷这块菜地的面积为________$\text{m}^2$.
(2)在上面【阅读】材料基础上,若$p = 5\text{cm}$,$a = 3\text{cm}$,$c = 4\text{cm}$,则此三角形的面积为________$\text{cm}^2$.
(3)如图是小明制作的一个风筝模型,其中$AB = BC = 50\text{cm}$,$AD = CD = 40\text{cm}$,$BD = 60\text{cm}$,请你用海伦公式帮助小明求风筝模型$ABCD$的面积为________$\text{cm}^2$.
答案:
(1)$12\sqrt{5}$
(2)$2\sqrt{5}$
(3)$750\sqrt{7}$
(1)$12\sqrt{5}$
(2)$2\sqrt{5}$
(3)$750\sqrt{7}$
查看更多完整答案,请扫码查看


