《2025年课堂点睛八年级数学下册人教版安徽专版》

1. 如图，正方形ABCD的边长为4，点E在边AB上，AE = 1，若点P为对角线BD上的一个动点，则△PAE周长的最小值是（ ）

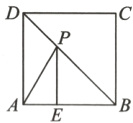
A. 3
B. 4
C. 5
D. 6

答案： D

2. 如图，点M是矩形ABCD的边AD的中点，P是BC边上的一动点，PE⊥MC于点E，PF⊥BM于点F.
(1)当矩形ABCD的长AD与宽AB满足什么条件时四边形PEMF为矩形？
(2)在(1)中当点P运动到什么位置时矩形PEMF变为正方形？为什么？

答案：
(1)解：当矩形ABCD的长AD与宽AB满足AD = 2AB时四边形PEMF为矩形，理由为：
∵四边形ABCD是矩形，
∴∠A = ∠D = 90°，AB = CD. 又
∵AD = 2AB，点M为AD的中点，
∴AM = DM = AB = CD，∠AMB = ∠DMC = 45°，
∴∠BMC = 90°. 又
∵PE⊥MC，PF⊥BM，
∴∠PEM = ∠PFM = 90°，
∴四边形PEMF为矩形.
(2)当点P运动到BC的中点时矩形PEMF变为正方形，理由：连接MP，
∵AB = AM = DM = CD，∠A = ∠D = 90°，
∴△ABM≌△DCM，
∴BM = CM. 又
∵点P为BC的中点，
∴∠BMP = ∠CMP. 又
∵PE⊥MC，PF⊥BM，
∴PE = PF，
∴矩形PEMF为正方形.

3. 如图，在四边形ABCD中，AD//BC，∠B = 90°，AB = 8cm，AD = 12cm，BC = 18cm，点P从点A出发以1cm/s的速度向点D运动；点Q从点C同时出发，以2cm/s的速度向点B运动，当点Q到达点B时，点P也停止运动，设点P，Q运动的时间为ts.
(1)从运动开始，当t取何值时，PQ//CD?
(2)在整个运动过程中是否存在t值，使得四边形PQCD是菱形？若存在，请求出t值；若不存在，请说明理由；
(3)从运动开始，当t取何值时，四边形PQBA是矩形？
(4)在整个运动过程中是否存在t值，使得四边形PQBA是正方形？若存在，请求出t值；若不存在，请说明理由.

答案：
(1)解：由题意知，AP = tcm，CQ = 2tcm，
∴DP = AD - AP = (12 - t)cm，
∵AD//BC，若要PQ//CD，则四边形PQCD为平行四边形，
∴DP = CQ，
∴12 - t = 2t，
∴t = 4，即t = 4时，PQ//CD.
(2)不存在，理由：
∵四边形PQCD是菱形，
∴CQ = CD，由题易知CD = 10，
∴2t = 10，
∴t = 5，此时DP = AD - AP = 12 - 5 = 7(cm)，而DP≠CD，
∴四边形PQCD不可能是菱形.
(3)
∵∠B = 90°，AD//BC，当AP = BQ时，四边形PQBA是矩形，即t = 18 - 2t，解得t = 6，当t = 6时，四边形PQBA是矩形.
(4)不存在. 理由：由t = 6时，四边形PQBA是矩形，可得AP = 6cm，
∵AB = 8cm，
∴AP≠AB，
∴矩形PQBA不能是正方形，即不存在时间t，使四边形PQBA是正方形.