《2025年课堂点睛八年级数学下册人教版安徽专版》

1.（甘肃省中考）如图，在四边形ABCD中，AB//DC，AD//BC，在不添加任何辅助线的前提下，要想四边形ABCD成为一个矩形，只需添加的一个条件是____________________.

答案： ∠B = 90°(答案不唯一)

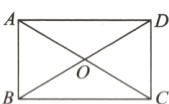
2.（贵州省中考）如图，四边形ABCD的对角线AC与BD相交于点O，AD//BC，∠ABC = 90°，有下列条件①AB//CD，②AD = BC.请从以上①②中任选1个作为条件，求证：四边形ABCD是矩形.

答案： 选择①，证明：
∵AB//CD，AD//BC，
∴四边形ABCD是平行四边形，又
∵∠ABC = 90°，
∴四边形ABCD是矩形；选择②，证明：
∵AD = BC，AD//BC，
∴四边形ABCD是平行四边形，又
∵∠ABC = 90°，
∴四边形ABCD是矩形.

3.（陕西省中考）在下列条件中，能够判定□ABCD是矩形的是（ ）
A. AB = AC
B. AC⊥BD
C. AB = AD
D. AC = BD

答案： D

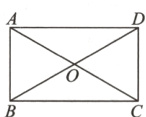
4.（长沙市中考）如图，□ABCD的对角线AC，BD相交于点O，△OAB是等边三角形，AB = 4.
（1）求证：□ABCD是矩形；
（2）求AD的长.

答案：
(1)证明：
∵△OAB是等边三角形，
∴OA = OB.
∵四边形ABCD是平行四边形，
∴OB = OD = $\frac{1}{2}$BD，OA = OC = $\frac{1}{2}$AC，
∴BD = AC，
∴▱ABCD是矩形.
(2)解：
∵四边形ABCD是矩形，
∴∠BAD = 90°.
∵△OAB是等边三角形，
∴∠ABO = 60°，
∴∠ADB = 90° - 60° = 30°，
∴BD = 2AB = 8，
∴AD = $\sqrt{BD^{2}-AB^{2}}=\sqrt{8^{2}-4^{2}} = 4\sqrt{3}$.

5.（情境题）小强用薄橡胶皮和布料自制了一块四边形鼠标垫.为了检验这块鼠标垫是不是矩形，他想出了以下几种方案，其中合理的是（ ）
A.测量对角线是否相等
B.测量两组对角是否相等
C.测量两组对边是否相等
D.测量其中的三个角是否都为直角

答案： D

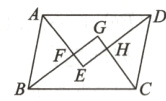
6.如图，在□ABCD中，四个内角的平分线交于点E，F，G，H.求证：四边形EFGH是矩形.

答案： 证明：
∵AB//CD，
∴∠ABC + ∠BCD = 180°，
∵BG平分∠ABC，CG平分∠BCD，
∴∠GBC = $\frac{1}{2}$∠ABC，∠GCB = $\frac{1}{2}$∠DCB，
∴∠GBC + ∠GCB = $\frac{1}{2}$∠ABC + $\frac{1}{2}$∠DCB = $\frac{1}{2}$(∠ABC + ∠DCB) = $\frac{1}{2}$×180° = 90°，
∴∠BGC = 90°，同理∠AFB = ∠AED = ∠DHC = 90°，
∴∠GFE = ∠AED = ∠GHE = 90°，
∴四边形EFGH是矩形.

7.下列命题正确的是（ ）
A.有一个角是直角的平行四边形是矩形
B.四条边相等的四边形是矩形
C.有一组邻边相等的平行四边形是矩形
D.对角线相等的四边形是矩形

答案： A