《2025年全优方案夯实与提高八年级数学下册浙教版》

9. 将多边形的边数由$n$条增加到$(n + x)$条后，内角和增加了$540^{\circ}$，则$x$的值为( ).
A. 1
B. 2
C. 3
D. 4

答案： C

10. 机器人在一平面上从点$A$处出发开始运动，规定“向前走1m再向左转$60^{\circ}$”为1次运动，则运动2024次后，机器人距离出发点$A$为( ).
A. 0m
B. 1m
C. $\sqrt{3}$m
D. 2m

答案： C

11. 如图，正五边形$FGHIJ$的顶点在正五边形$ABCDE$的边上，若$\angle1 = 20^{\circ}$，则$\angle2=$________。
　　　　　　

答案： 52°

12. 如图1，圆上均匀分布着11个点$A_1$，$A_2$，$A_3$，…，$A_{11}$。从点$A_1$起每隔$k$个点顺次连结，当再次与点$A_1$连结时，我们把所形成的图形称为“$k + 1$阶正十一角星”，其中$1\leqslant k\leqslant8$（$k$为正整数）。例如，图2是“2阶正十一角星”，那么$\angle A_1+\angle A_2+\cdots+\angle A_{11}=$________。
　　　

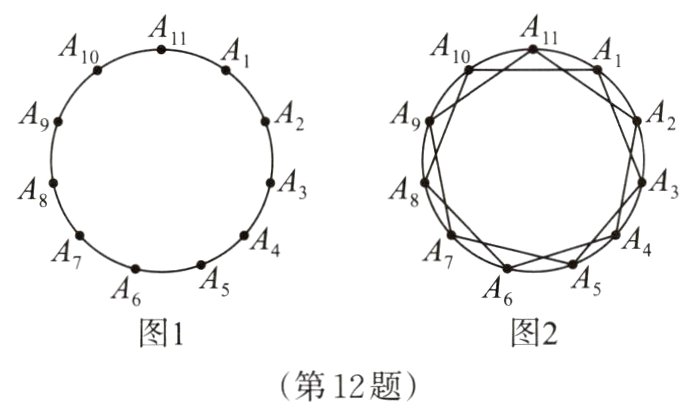
答案： 1260°

13. 如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形。如图所示为一组正多边形，观察每个正多边形中$\angle\alpha$的变化情况，解答下列问题：
　　　　　　
(1)将下面的表格补充完整：
|正多边形的边数|3|4|5|6|…|$n$|
|----|----|----|----|----|----|----|
|$\angle\alpha$的度数|$60^{\circ}$|$45^{\circ}$| | |…| |
　　　
(2)根据规律，是否存在一个正多边形使得$\angle\alpha = 21^{\circ}$？若存在，请求出$n$的值；若不存在，请说明理由。

答案：
(1)36°　30°　($\frac{180}{n}$)°
(2)不存在,理由如下:设存在正n边形使得∠α=21°,则∠α=21°=($\frac{180}{n}$)°,解得n=8$\frac{4}{7}$.
∵n是正整数,
∴n=8$\frac{4}{7}$不符合题意，要舍去.
∴不存在正n边形使得∠α=21°.