《2025年全优方案夯实与提高八年级数学下册浙教版》

18. （8分）某中学八年级举行跳绳比赛，要求每班选出5名学生参加，在规定时间内跳绳不低于150次为优秀，冠、亚军在八（1）班和八（5）班中产生. 下表是这两个班的5名学生的比赛数据（单位：次）：

（1）求两班的优秀率及两班数据的中位数.
（2）请你从优秀率、中位数和方差三方面进行简要分析，确定获得冠军的班级.

答案：
(1)八
(1)班的优秀率：$\frac{3}{5}\times100\% = 60\%$，
八
(5)班的优秀率：$\frac{2}{5}\times100\% = 40\%$；
八
(1)班数据的中位数为150次，八
(5)班数据的中位数为147次.
(2)从优秀率看，八
(1)班的优秀人数多；从中位数看，八
(1)班较大，一般水平较高；从方差看，八
(1)班的成绩比八
(5)班的稳定，所以八
(1)班获得冠军.

19. （8分）某食品商店将甲、乙、丙3种糖果按5:4:1的质量比配制成一种什锦糖果. 已知甲、乙、丙三种糖果的单价分别为16元/千克、20元/千克、27元/千克，若将这种什锦糖果的单价定为这三种糖果单价的算术平均数，你认为合理吗？如果合理，请说明理由；如果不合理，请求出该什锦糖果合理的单价.

答案： 这样定价不合理，理由如下：
加权平均数：$16\times\frac{5}{10}+20\times\frac{4}{10}+27\times\frac{1}{10}=18.7$(元/千克)，算术平均数：$\frac{16 + 20 + 27}{3}=21$(元/千克)，
$\because 21＞18.7$，$\therefore$将这种什锦糖果的单价定为这三种糖果单价的算术平均数不合理.
$\therefore$该什锦糖果合理的单价为18.7元/千克.

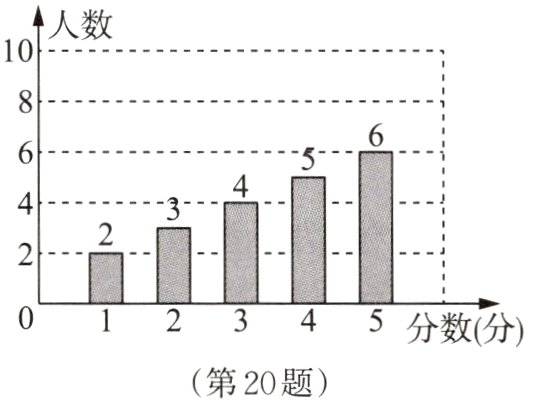
20. （8分）为了解某电影在“五一”假期的上映满意度，某数学小组随机抽取了部分观众对这部电影进行打分（打分按从高到低分为5个分值：5分、4分、3分、2分、1分），根据调查结果，绘制出如图所示的统计图.
（1）分别求这组打分数据的平均数、中位数和众数.
（2）该小组后来又另外随机抽取几名观众对这部电影进行打分，得知这几名观众的打分均小于4分，将这次打分的数据与之前的数据合并后发现中位数发生了改变，那么后来最少随机抽取了________名观众.

答案：
(1)这组打分数据的平均数为$\frac{1}{20}\times(1\times2 + 2\times3 + 3\times4 + 4\times5 + 5\times6)=3.5$(分).
$\because$数据的个数是20，
$\therefore$中位数是第10、11个数的平均数.
$\therefore$这组打分数据的中位数是$\frac{4 + 4}{2}=4$(分).
$\because$这组打分数据中5出现的次数最多，
$\therefore$这组打分数据的众数是5分.
(2)设后来随机抽取了$x$名观众.
由题意得$2 + 3 + 4 + x\geq5 + 6$，解得$x\geq2$.
$\therefore$后来最少随机抽取了2名观众.
故答案为：2.

21. （8分）某校开展消防知识竞赛，参加知识竞赛的学生被分为甲、乙两组，每组学生均为20名，赛后根据竞赛成绩得到尚不完整的统计图表（如图），已知竞赛成绩满分为100分，统计表中$a$，$b$满足$b = 2a$.
成绩（分）　　70　　　　80　　　　90　　　　100
人数　　　　3　　　　$a$　　　　$b$　　　　5　　　　　　　　　　　　　口S71404分°

（1）求统计表中$a$，$b$的值.
（2）小明按以下方法计算甲组20名学生竞赛成绩的平均分：$(70 + 80 + 90 + 100)\div4 = 85$（分）. 根据所学统计知识判断小明的计算是否正确，若不正确，请写出正确的算式并计算出结果.
（3）如果依据平均成绩确定竞赛结果，那么竞赛成绩较好的是哪个组？请说明理由.

答案：
(1)$\because$每组学生均为20名，$\therefore a + b = 20 - 3 - 5 = 12$.$\because b = 2a$，$\therefore a = 4$，$b = 8$.
(2)小明的计算不正确，正确的计算如下：
$\frac{70\times3 + 80\times4 + 90\times8 + 100\times5}{20}=87.5$(分).
(3)竞赛成绩较好的是甲组.理由如下：
乙组20名学生竞赛成绩的平均分：$100\times\frac{360 - 90 - 90 - 144}{360}+90\times\frac{90}{360}+80\times\frac{90}{360}+70\times\frac{144}{360}=10 + 22.5 + 20 + 28 = 80.5$(分).
$\because 80.5＜87.5$，$\therefore$竞赛成绩较好的是甲组.