《2025年实验班提优大考卷九年级数学上册苏科版》

9. 实验班原创 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$a$、$b$、$c$分别是$\angle A$、$\angle B$、$\angle C$的对边,若$4a = 3b$,则$\sin B$的值是$\frac45$.

答案： 9.$\frac45$ [解析]由题可知，在$Rt\triangle ABC$中，$\angle C=90°$，a、b、c分别是$\angle A$、$\angle B$、$\angle C$的对边，$4a=3b$.
令$b=4x$，则$a=3x$，由勾股定理，得$c=5x$，
所以$\sin B=\frac{b}c=\frac{4x}{5x}=\frac45$.

10. (2025·无锡外国语学校期中改编)小红沿坡比为$1:\sqrt{3}$的斜坡上走了 120 米,则她实际上升了60米.

答案： 10.60 [解析]小红沿坡比为$1:\sqrt3$的斜坡上走了120米，设竖直距离为x，则水平距离为$\sqrt3x$，
根据题意，得$x^2+(\sqrt3x)^2=120^2$，解得$x=60$(负值舍去)，
$\therefore$她实际上升了60米.

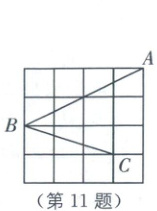
11. 如图,在网格中,每个小正方形的边长均为 1,每个小正方形的顶点称为格点,点$A$、$B$、$C$三点都在格点上,则$\sin\angle ABC =$$\frac{\sqrt2}2$.

答案： 11.$\frac{\sqrt2}2$
[解析]连接AC.
由勾股定理，得$AB^2=2^2+4^2=20$，$BC^2=1^2+3^2=10$，$AC^2=1^2+3^2=10$，则$BC^2+AC^2=AB^2$，$\therefore \angle ACB=90°$，
$\therefore \sin\angle ABC=\frac{AC}{AB}=\frac{\sqrt{10}}{2\sqrt5}=\frac{\sqrt2}2$.

12. 已知$\tan(\alpha + 15^{\circ})=\sqrt{3}$,则$\tan\alpha$的值为1.

答案： 12.1 [解析]$\because \tan60°=\sqrt3$，$\therefore \alpha+15°=60°$，
解得$\alpha=45°$，$\therefore \tan\alpha=1$.

13. 在$\triangle ABC$中,若$\left|\sin A-\frac{1}{2}\right|+\left(\cos B-\frac{\sqrt{3}}{2}\right)^{2}=0$,则$\triangle ABC$的形状是等腰三角形.

答案： 13.等腰三角形 [解析]
∵$\vert\sin A-\frac12\vert+(\cos B-\frac{\sqrt3}2)^2=0$，
$\therefore \sin A-\frac12=0$，$\cos B-\frac{\sqrt3}2=0$，
$\therefore \sin A=\frac12$，$\cos B=\frac{\sqrt3}2$，$\therefore \angle A=30°$，$\angle B=30°$，
$\therefore \triangle ABC$的形状是等腰三角形.

14. (2025·常州武进区期中)如图,在$\triangle ABC$中,$AB = BC$,$\tan B=\frac{5}{12}$,$D$为$BC$上一点,若满足$CD=\frac{5}{8}BD$,过点$D$作$DE\perp AD$交$AC$延长线于点$E$,则$\frac{CE}{AC}=$$\frac{20}{21}$.

答案：
14.$\frac{20}{21}$ [解析]如图，过点A作$AH\perp CB$于点H，作$CM\perp AD$于点M.

$\because AB=BC$，$CD=\frac58BD$，$\therefore$设$BD=8a$，则$CD=5a$，
$\therefore BC=AB=BD+CD=13a$.
$\because \tan B=\frac{AH}{BH}=\frac5{12}$，$\therefore AH=5a$，$BH=12a$，
$\therefore DH=BH-BD=4a$，$CH=a$，
在$Rt\triangle ACH$中，$AC=\sqrt{AH^2+CH^2}=\sqrt{26}a$，
在$Rt\triangle ADH$中，$AD=\sqrt{AH^2+DH^2}=\sqrt{41}a$，
$\therefore \cos\angle ADC=\frac{DH}{AD}=\frac{4\sqrt{41}}{41}$，
$\therefore DM=CD· \cos\angle ADC=\frac{20\sqrt{41}}{41}a$，
$\therefore AM=AD-DM=\frac{21\sqrt{41}}{41}a$.
$\because CM\perp AD$，$DE\perp AD$，$\therefore \triangle AMC\sim\triangle ADE$，
$\therefore \frac{CE}{AC}=\frac{DM}{AM}=\frac{20}{21}$.

15. 跨学科 力的作用 (2024·福建中考)无动力帆船是借助风力前行的.如图是帆船借助风力航行的平面示意图,已知帆船航行方向与风向所在直线的夹角$\angle PDA$为$70^{\circ}$,帆与航行方向的夹角$\angle PDQ$为$30^{\circ}$,风对帆的作用力$F$为$400\ N$.根据物理知识,$F$可以分解为两个力$F_{1}$与$F_{2}$,其中与帆平行的力$F_{1}$不起作用,与帆垂直的力$F_{2}$又可以分解为两个力$f_{1}$与$f_{2}$,$f_{1}$与航行方向垂直,被舵的阻力抵消;$f_{2}$与航行方向一致,是真正推动帆船前行的动力.在物理学上常用线段的长度表示力的大小,据此,建立数学模型:$F = AD = 400$,则$f_{2}=CD=$128.(单位:N,参考数据:$\sin40^{\circ}\approx0.64$,$\cos40^{\circ}\approx0.77$)

答案：
15.128 [解析]如图，令$\angle PDQ$的对顶角为$\angle1$.

$\because \angle PDA=70°$，$\angle PDQ=30°$，
$\therefore \angle ADQ=\angle PDA-\angle PDQ=70°-30°=40°$，$\angle1=\angle PDQ=30°$.$\because AB// QD$，$\therefore \angle BAD=\angle ADQ=40°$.
在$Rt\triangle ABD$中，$AD=400$，$\angle ABD=90°$，
$\therefore BD=AD· \sin\angle BAD=400· \sin40°\approx400×0.64=256$.由题意可知，$BD\perp DQ$，$\therefore \angle BDC+\angle1=90°$，
在$Rt\triangle BCD$中，$BD=256$，$\angle BCD=90°$，
$\therefore CD=BD· \cos\angle BDC=256×\cos60°=256×\frac12=128$.

16. 动点定圆模型 (2024·烟台中考)如图,在$□ ABCD$中,$\angle C = 120^{\circ}$,$AB = 8$,$BC = 10$.$E$为边$CD$的中点,$F$为边$AD$上的一动点,将$\triangle DEF$沿$EF$翻折得$\triangle D'EF$,连接$AD'$、$BD'$,则$\triangle ABD'$面积的最小值为$20\sqrt3-16$.

答案：
16.$20\sqrt3-16$ [解析]在$□ ABCD$中，$\angle BCD=120°$，$AB=8$，$\therefore CD=AB=8$，$AB// CD$，则$\angle ABC=180°-\angle BCD=60°$.
$\because$E为边CD的中点，$\therefore DE=CE=\frac12CD=4$.
$\because \triangle DEF$沿EF翻折得$\triangle D'EF$，$\therefore ED'=DE=4$，

$\therefore$点$D'$在以E为圆心，4为半径的圆上运动，如图，过点E作$EM\perp AB$交BA延长线于点M，交圆E于点G，此时点G到边AB的距离最短，最小值为GM的长，则当$D'$在点G时$\triangle ABD'$的面积最小.
过点C作$CN\perp AB$于点N.$\because AB// CD$，$\therefore EM=CN$.
在$Rt\triangle BCN$中，$BC=10$，$\angle CBN=60°$，
$\therefore CN=BC· \sin60°=10×\frac{\sqrt3}2=5\sqrt3$，
$\therefore GM=ME-EG=5\sqrt3-4$，$\therefore \triangle ABD'$面积的最小值为$\frac12×8×(5\sqrt3-4)=20\sqrt3-16$.

17. 中考新考法 最值问题 (2025·苏州工业园区期中)如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AB = 5$,$BC = 3$,点$D$是斜边$AB$上任意一点,连接$CD$,过点$C$作$CE\perp CD$于点$C$,连接$DE$,使得$\angle EDC = \angle A$.当$\triangle BDE$的面积取得最大值时,$\tan\angle BCE$的值为$\frac34$.

答案： 17.$\frac34$
[解析]
∵$CE\perp CD$，$\angle ACB=90°$，
$\therefore \angle BCE+\angle BCD=90°$，$\angle ACD+\angle BCD=90°$，
$\therefore \angle BCE=\angle ACD$.
在$Rt\triangle ABC$中，$\angle ACB=90°$，$AB=5$，$BC=3$，
由勾股定理，得$AC=\sqrt{AB^2-BC^2}=4$.
在$Rt\triangle CDE$中，$\tan\angle EDC=\frac{CE}{CD}$.
在$Rt\triangle ABC$中，$\tan A=\frac{BC}{AC}$.
$\because \angle EDC=\angle A$，$\therefore \frac{CE}{CD}=\frac{BC}{AC}$.
$\because \angle BCE=\angle ACD$，$\therefore \triangle BCE\sim\triangle ACD$.
$\therefore \frac{BE}{AD}=\frac{BC}{AC}=\frac34$，$\angle CBE=\angle A$，
$\therefore$设$BE=3x$，$AD=4x$，$\therefore BD=AB-AD=5-4x$.
$\because \angle A+\angle ABC=90°$，$\therefore \angle CBE+\angle ABC=90°$，
即$\angle ABE=90°$.
设$\triangle BDE$的面积为S，
则$S=\frac12BD· BE=\frac12×3x(5-4x)$，
整理，得$S=-6x^2+\frac{15}2x=-6(x-\frac58)^2+\frac{75}{32}$，
$\therefore$当$x=\frac58$时，S最大，此时$AD=4x=4×\frac58=\frac52$.
$\because AB=5$，$\therefore AD=\frac12AB$，
$\therefore$当点D是$Rt\triangle ABC$斜边的中点时，$\triangle BDE$的面积取得最大值，此时$CD=AD=BD$，$\therefore \angle A=\angle ACD=\angle BCE$.
$\because \tan A=\frac{BC}{AC}=\frac34$，$\therefore \tan\angle BCE=\frac34$.

18. (2023·广元中考)如图,在平面直角坐标系中,已知点$A(1,0)$,点$B(0,-3)$,点$C$在$x$轴上,且点$C$在点$A$右方,连接$AB$、$BC$,若$\tan\angle ABC=\frac{1}{3}$,则点$C$的坐标为$(\frac94,0)$.

答案：
18.$(\frac94,0)$ [解析]设$C(a,0)$，
$\therefore OC=a$.
$\because$点$A(1,0)$，点$B(0,-3)$，
$\therefore OA=1$，$AC=a-1$，$OB=3$，
$BC=\sqrt{3^2+a^2}=\sqrt{a^2+9}$.
在$Rt\triangle OAB$中，$\tan\angle OBA=\frac{OA}{OB}=\frac13$，又$\tan\angle ABC=\frac13$，
$\therefore \angle OBA=\angle ABC$.

如图，过点C作$CD// y$轴交BA的延长线于点D，
$\therefore \angle OBA=\angle D$，$\angle AOB=\angle ACD$，
$\therefore \triangle OBA\sim\triangle CDA$，$\therefore \frac{OB}{CD}=\frac{OA}{CA}$，$CD=BC$，$\therefore \frac{OB}{BC}=\frac{OA}{AC}$，
$\therefore \frac{3}{\sqrt{a^2+9}}=\frac1{a-1}$，解得$a=0$(舍去)或$a=\frac94$，
$\therefore C(\frac94,0)$.