《2025年实验班提优大考卷九年级数学上册苏科版》

25. （8分）悠悠食品店的$A$、$B$两种菜品，每份成本均为$14$元，售价分别为$20$元、$18$元，这两种菜品每天的营业额共为$1120$元，总利润为$280$元.
（1）该店每天卖出这两种菜品共多少份？
（2）该店为了增加利润，准备降低$A$种菜品的售价，同时提高$B$种菜品的售价，售卖时发现，$A$种菜品售价每降$0.5$元可多卖$1$份；$B$种菜品售价每提高$0.5$元就少卖$1$份，如果这两种菜品每天销售的总份数不变，这两种菜品一天的总利润是$316$元. 求$A$种菜品每天销售多少份？

答案： 25.
(1)设该店每天卖出$A$、$B$两种菜品分别为$x$份、$y$份. 根据题意，得$\begin{cases}(20 - 14)x+(18 - 14)y=280\\20x + 18y=1120\end{cases}$，解得$\begin{cases}x = 20\\y = 40\end{cases}$，$\therefore x + y = 60$. 故该店每天卖出这两种菜品共60份.
(2)设$A$种菜品售价降$0.5a$元，即每天卖$(20 + a)$份，则$B$种菜品卖$(40 - a)$份，每份售价提高$0.5a$元. 根据题意，得$(20 - 14 - 0.5a)(20 + a)+(18 - 14 + 0.5a)·(40 - a)=316$，即$a^{2}-12a + 36=0$，解得$a_{1}=a_{2}=6,\therefore 20 + a = 26$. 故$A$种菜品每天销售26份.

26. （8分）如图，$C$、$D$是以$AB$为直径的半圆上的两点，$\angle CAB = \angle DBA$，连接$BC$、$CD$.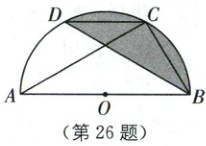
（1）求证：$CD // AB$；
（2）若$AB = 4$，$\angle ACD = 30°$，求阴影部分的面积.

答案：
26.
(1)$\because \overset\frown{AD}=\overset\frown{AD},\therefore \angle ACD=\angle DBA$. 又$\angle CAB=\angle DBA,\therefore \angle CAB=\angle ACD,\therefore CD// AB$.
(2)如图，连接$OD$，过点$D$作$DE\perp AB$，垂足为$E$. $\because \angle ACD=30^{\circ},\therefore \angle AOD=120^{\circ}$. $\because AB = 4$，$\therefore OA=OB=OD=2$，$\therefore S_{扇形ODB}=\frac{n\pi r^{2}}{360}=\frac{120×\pi×2^{2}}{360}=\frac{4}{3}\pi$. 在$ Rt\triangle BDO$中，$\because \angle AOD=60^{\circ},\therefore \angle ODE=30^{\circ}$，$\therefore OE=\frac{1}{2}OD=1,\therefore DE=\sqrt{OD^{2}-OE^{2}}=\sqrt{3}$，$\therefore S_{\triangle BOD}=\frac{1}{2}× OB× DE=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$，$\therefore S_{阴影}=S_{扇形ODB}-S_{\triangle BOD}=\frac{4}{3}\pi-\sqrt{3}$.

27. （10分）（2025·宿迁宿城区期中）《朗读者》自开播以来，以其厚重的文化底蕴和感人的人文情怀，感动了数以亿计的观众，某中学开展“朗读”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出$5$名选手参加复赛，两个班各选出的$5$名选手的复赛成绩（满分为$100$分）如图所示.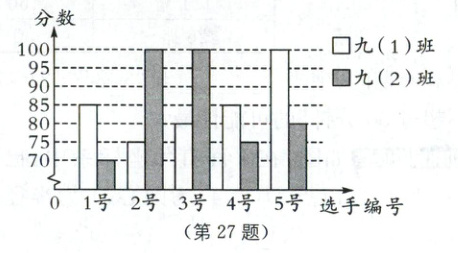
（1）根据图示填写表格.

（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好.
（3）如果规定成绩较稳定班级胜出，你认为哪个班级能胜出？说明理由.

答案： 27.
(1)九
(1)班5位同学的成绩为75、80、85、85、100，中位数为85分. 九
(2)班5位同学的成绩为70、100、100、75、80，$\therefore$九
(2)班的平均数为$\frac{1}{5}×(70 + 100 + 100 + 75 + 80)=85( 分)$，其众数为100. 补全表格如下： | | 平均数 | 中位数 | 众数 | | --- | --- | --- | --- | | 九
(1)班 | 85 | 85 | 85 | | 九
(2)班 | 85 | 80 | 100 |
(2)九
(1)班成绩好些.$\because$两个班的平均数相同，而九
(1)班的中位数高，$\therefore$在平均数相同的情况下，中位数高的九
(1)班成绩好些.
(3)九
(1)班的成绩更稳定，能胜出.理由如下： $\because s_{九(1)}^{2}=\frac{1}{5}×[(75 - 85)^{2}+(80 - 85)^{2}+(85 - 85)^{2}+(85 - 85)^{2}+(100 - 85)^{2}]=70$， $s_{九(2)}^{2}=\frac{1}{5}×[(70 - 85)^{2}+(100 - 85)^{2}+(100 - 85)^{2}+(75 - 85)^{2}+(80 - 85)^{2}]=160$， $\therefore s_{九(1)}^{2}＜s_{九(2)}^{2},\therefore$九
(1)班的成绩更稳定，能胜出.