《2025年实验班提优大考卷九年级数学上册苏科版》

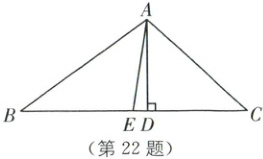
22. (8分)(2024·浙江中考)如图,在$\triangle ABC$中$,AD\perp BC$,$AE$是边$BC$上的中线$,AB = 10,AD = 6,\tan\angle ACB = 1$.
(1)求$BC$的长;
(2)求$\sin\angle DAE$的值.

答案： 22.
(1)
∵AD⊥BC,AB = 10,AD = 6,
∴BD = $\sqrt{AB^2 - AD^2} = \sqrt{10^2 - 6^2} = 8$.
∵$\tan \angle ACB = 1$,
∴CD = AD = 6,
∴BC = BD + CD = 8 + 6 = 14.
(2)
∵AE是边BC上的中线,
∴CE = $\frac{1}{2} BC = 7$,
∴DE = CE - CD = 7 - 6 = 1.
∵AD⊥BC,
∴AE = $\sqrt{AD^2 + DE^2} = \sqrt{6^2 + 1^2} = \sqrt{37}$,
∴$\sin \angle DAE = \frac{DE}{AE} = \frac{1}{\sqrt{37}} = \frac{\sqrt{37}}{37}$.

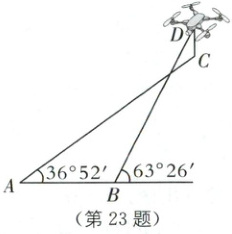
23. (8分)(2023·南京中考)如图,为了测量无人机的飞行高度,在水平地面上选择观测点$A$、$B$.无人机悬停在$C$处,此时在$A$处测得$C$的仰角为$36^{\circ}52'$;无人机垂直上升$5\ m$悬停在$D$处,此时在$B$处测得$D$的仰角为$63^{\circ}26'$.$AB = 10\ m$,点$A$、$B$、$C$、$D$在同一平面内$,A$、$B$两点在$CD$的同侧.求无人机在$C$处时离地面的的高度.(参考数据:$\tan 36^{\circ}52'\approx0.75,\tan 63^{\circ}26'\approx2.00$)

答案：
23.如图,延长DC交AB于点E.

由题意,得DE⊥AB,CD = 5m,设BE = xm,
∵AB = 10m,
∴AE = AB + BE = (10 + x)m.
在Rt△ACE中,∠CAE = 36°52′,
∴CE = AE·$\tan 36°52′ \approx 0.75(10 + x)$m.
在Rt△BDE中,∠DBE = 63°26′,
∴DE = BE·$\tan 63°26′ \approx 2x$(m).
∵DC + CE = DE,
∴5 + 0.75(10 + x) = 2x,
解得x = 10,
∴CE = 0.75(10 + x) = 15(m).
∴无人机在C处时离地面的高度约为15m.

24. (8分)Z字型 (2025·广东广州增城区模拟)如图是一名军事迷设计的潜水望远镜,$MN// GA// PQ// BH$,$AB// NP$,两个反光镜$KI// CD$,直线$MN$、$GA$之间的距离为$5\ cm$,$\angle MNP = 122^{\circ}$.与$MN$平行的一束光线经两个反光镜反射后沿$O_2F$射出,其中$O_1O_2// AB$.(参考值:$\sin 29^{\circ}\approx0.49,\cos 29^{\circ}\approx0.87$,$\tan 29^{\circ}\approx0.55,\sin 58^{\circ}\approx0.85,\cos 58^{\circ}\approx0.53,\tan 58^{\circ}\approx1.60$)
(1)当$G$、$A$、$I$三点共线时,求反光镜$KI$的长度;(结果保留一位小数)
(2)当$G$、$A$、$I$三点共线时,已知$AB = 4$米,求点$A$到直线$BH$的距离.

答案：
24.
(1)如图,过点K作KS⊥AG,垂足为S.

∵MN//EO₁,O₁O₂//AB//NP,
∴∠KO₁E = ∠NKI,∠IO₁O₂ = ∠NIK.
由题意,得∠KO₁E = ∠IO₁O₂,
∴∠NIK = ∠NKI = $\frac{1}{2}$(180° - ∠MNP) = 29°.
∵MN//GA,
∴∠KIS = ∠NKI = 29°.
在Rt△KSI中,KI = $\frac{KS}{\sin 29°} \approx \frac{5}{0.49} \approx 10.2$(cm),
∴反光镜KI的长度为10.2cm.
(2)过点A作AT⊥BH,垂足为T.
∵MN//GI,
∴∠AIP = ∠MNP = 122°.
∵AB//NP,
∴∠GAB = ∠AIP = 122°.
∵GA//BH,
∴∠GAB + ∠ABT = 180°.
∴∠ABT = 180° - 122° = 58°.
在Rt△ATB中,
AT = AB·$\sin \angle ABT$ = AB·$\sin 58° \approx 4 × 0.85 = 3.4$(m),
∴点A到直线BH的距离为3.4m.