第142页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
22. (8分)为了增强学生保护环境的意识,在6月5日“世界环境日”当天,某校在七、八年级举行了环保知识竞赛,现从七、八年级所有参赛学生中各随机抽取了10名学生的成绩(百分制)进行整理和分析,部分信息如下所示:[说明:七、八年级全体参赛学生的竞赛成绩分成了$A$、$B$、$C$、$D$四个分数段,各分数段成绩取值范围为(成绩用$x$表示,单位:分)$A:60\leqslant x<70$,$B:70\leqslant x<80$,$C:80\leqslant x<90$,$D:90\leqslant x\leqslant100$].
[收集数据]七年级10名同学竞赛成绩如下:75、84、78、72、91、79、86、69、72、94.
八年级10名同学竞赛成绩中落在$C$分数段的成绩如下:80、82、82、84、85.
[整理数据]七、八年级各10名学生竞赛成绩在四个分数段的分布如下表所示:

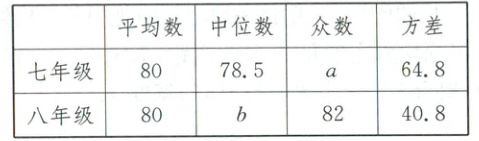
[分析数据]七、八年级各10名学生竞赛成绩的平均数、中位数、众数、方差如下表:
[问题解决]根据以上信息,解答下列问题:
(1)填空:$a =$,$b =$.
(2)若该校七年级共有300名学生参加了知识竞赛,请估计七年级所有参赛学生中成绩达优良(满足$x\geqslant80$即为优良)的人数.
(3)根据以上数据分析,你认为哪个年级所抽取的10名学生竞赛成绩更好?请说明理由.
[收集数据]七年级10名同学竞赛成绩如下:75、84、78、72、91、79、86、69、72、94.
八年级10名同学竞赛成绩中落在$C$分数段的成绩如下:80、82、82、84、85.
[整理数据]七、八年级各10名学生竞赛成绩在四个分数段的分布如下表所示:

[分析数据]七、八年级各10名学生竞赛成绩的平均数、中位数、众数、方差如下表:

[问题解决]根据以上信息,解答下列问题:
(1)填空:$a =$,$b =$.
(2)若该校七年级共有300名学生参加了知识竞赛,请估计七年级所有参赛学生中成绩达优良(满足$x\geqslant80$即为优良)的人数.
(3)根据以上数据分析,你认为哪个年级所抽取的10名学生竞赛成绩更好?请说明理由.
答案:
22.[解析]本题考查中位数、算术平均数、众数及方差,解题的关键是掌握众数、中位数的定义及方差的意义.
(1)根据众数和中位数的定义求解即可;
(2)总人数乘样本中七年级成绩优良人数所占比例即可;
(3)根据中位数、平均数及方差的意义求解即可.
解:
(1)$72$ $81$ 提示:七年级成绩的众数$a = 72$,八年级成绩的中位数$b=\frac{80 + 82}{2}=81$.
(2)$300×\frac{2 + 2}{10}=120$(名),故估计七年级所有参赛学生中成绩达优良(满足$x\geq80$即为优良)的人数约有$120$.
(3)八年级成绩更好,因为七、八年级成绩的平均数相等,而八年级成绩的中位数大于七年级,方差小于七年级,所以八年级高分人数多于七年级,稳定性更好.
知识拓展 统计的特征量:平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.方差是各数据与差的平方的平均数,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据波动越大,数据越不稳定;反之,方差越小,表明这组数据波动越小,数据越稳定.
(1)根据众数和中位数的定义求解即可;
(2)总人数乘样本中七年级成绩优良人数所占比例即可;
(3)根据中位数、平均数及方差的意义求解即可.
解:
(1)$72$ $81$ 提示:七年级成绩的众数$a = 72$,八年级成绩的中位数$b=\frac{80 + 82}{2}=81$.
(2)$300×\frac{2 + 2}{10}=120$(名),故估计七年级所有参赛学生中成绩达优良(满足$x\geq80$即为优良)的人数约有$120$.
(3)八年级成绩更好,因为七、八年级成绩的平均数相等,而八年级成绩的中位数大于七年级,方差小于七年级,所以八年级高分人数多于七年级,稳定性更好.
知识拓展 统计的特征量:平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.方差是各数据与差的平方的平均数,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据波动越大,数据越不稳定;反之,方差越小,表明这组数据波动越小,数据越稳定.
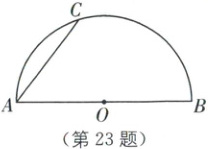
23. (8分) 中考新考法 尺规作图 如图,$AB$是半圆的直径,点$O$为圆心,$C$是半圆上一点,连接$AC$.
(1)用无刻度的直尺和圆规作图:在半圆上确定一点$P$,使得$\overset{\frown}{PB}=\overset{\frown}{PC}$(保留作图痕迹);
(2)在(1)的条件下,连接$PB$、$PC$,若$AB = 10$,$AC = 6$,求四边形$ABPC$的面积.
(1)用无刻度的直尺和圆规作图:在半圆上确定一点$P$,使得$\overset{\frown}{PB}=\overset{\frown}{PC}$(保留作图痕迹);
(2)在(1)的条件下,连接$PB$、$PC$,若$AB = 10$,$AC = 6$,求四边形$ABPC$的面积.

答案:
23.[解析]本题考查作图——复杂作图、圆心角、弧、弦之间的关系、圆周角定理、点与圆的位置关系,解题的关键是理解题意,灵活运用所学知识解决问题.
(1)分别以点$B$、$C$为圆心,大于$\frac{1}{2}BC$长为半径画弧,交于点$D$,连接$OD$交圆于点$P$,则点$P$即为所求;
(2)利用勾股定理求出$BC$,再求出$PH$,利用三角形面积公式求解即可.
解:
(1)如图,点$P$即为所求;

$\rightarrow$利用垂径定理
(2)$\because AB$是直径,$\therefore\angle ACB = 90^{\circ}$,
$\therefore BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-6^{2}}=8$.
$\because OP\perp BC$,$\therefore CH = BH$.$\because OA = OB$,
$\therefore OH=\frac{1}{2}AC = 3$.$\because OP = 5$,$\therefore PH = OP - OH = 5 - 3 = 2$,$\therefore$四边形$ABPC$的面积$=\frac{1}{2}AC· BC+\frac{1}{2}BC· PH=\frac{1}{2}×6×8+\frac{1}{2}×8×2 = 32$.
一题多解
(1)如图,作$\angle BAC$的平分线交$\odot O$于点$P$,点$P$即为所求.

23.[解析]本题考查作图——复杂作图、圆心角、弧、弦之间的关系、圆周角定理、点与圆的位置关系,解题的关键是理解题意,灵活运用所学知识解决问题.
(1)分别以点$B$、$C$为圆心,大于$\frac{1}{2}BC$长为半径画弧,交于点$D$,连接$OD$交圆于点$P$,则点$P$即为所求;
(2)利用勾股定理求出$BC$,再求出$PH$,利用三角形面积公式求解即可.
解:
(1)如图,点$P$即为所求;

$\rightarrow$利用垂径定理
(2)$\because AB$是直径,$\therefore\angle ACB = 90^{\circ}$,
$\therefore BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-6^{2}}=8$.
$\because OP\perp BC$,$\therefore CH = BH$.$\because OA = OB$,
$\therefore OH=\frac{1}{2}AC = 3$.$\because OP = 5$,$\therefore PH = OP - OH = 5 - 3 = 2$,$\therefore$四边形$ABPC$的面积$=\frac{1}{2}AC· BC+\frac{1}{2}BC· PH=\frac{1}{2}×6×8+\frac{1}{2}×8×2 = 32$.
一题多解
(1)如图,作$\angle BAC$的平分线交$\odot O$于点$P$,点$P$即为所求.

查看更多完整答案,请扫码查看


