《2025年实验班提优大考卷九年级数学上册苏科版》

12.若$\sin A=\frac{2}{3}$,则$\tan A$的值为$\frac{2\sqrt{5}}{5}$。

答案： 12.$\frac{2\sqrt{5}}{5}$ [解析]本题考查了同角三角函数关系、勾股定理.
直接利用已知结合勾股定理表示出AC、BC的长，再利用锐角三角函数关系得出答案.
在三角形ABC中，假设$\angle C=90^{\circ}$，设$BC=2x$.$\because \sin A=\frac{BC}{AB}=\frac{2}{3}$，$\therefore AB=3x$.则$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{5}x$，
$\therefore \tan A=\frac{BC}{AC}=\frac{2x}{\sqrt{5}x}=\frac{2\sqrt{5}}{5}$.
知识拓展 在$Rt\triangle ABC$中，若$\angle C=90^{\circ}$，则$\angle A$的正弦等于$\angle A$的对边比斜边，$\angle A$的余弦等于$\angle A$的邻边比斜边，$\angle A$的正切等于$\angle A$的对边比邻边.即$\sin A=\frac{\angle A的对边}{斜边}$，$\cos A=\frac{\angle A的邻边}{斜边}$，$\tan A=\frac{\angle A的对边}{\angle A的邻边}$.

13.一个圆锥的底面半径为 3,高为 4,则此圆锥的侧面积为15π。

答案： 13.$15\pi$ [解析]本题考查了圆锥的计算，首先根据底面半径和高利用勾股定理求得母线长，然后直接利用圆锥的侧面积公式代入求出即可.$\because$圆锥的底面半径为3，高为4，
$\therefore$母线长$l$为5，$\therefore$圆锥的侧面积为$\pi rl=\pi × 3× 5=15\pi$.

14.数形结合思想 若某飞机落地时,飞机在地面滑行距离$s( 米)$与滑行时间$t( 秒)$的关系近似满足$s=-2(t-15)^{2}+200$,则该飞机从落地到停止,在地面滑行的时间为15秒。

答案： 14.15 [解析]本题考查二次函数的应用，根据二次函数顶点式的含义进行分析即可.由于二次项系数为负，存在最大值，函数的顶点坐标为$(15,200)$，$\therefore$当$t=15$秒时，滑行距离最大.因此，飞机从落地到停止滑行的时间为15秒.

15.如图,$\odot O$的直径$AB=6$,$AD$、$BC$是它的两条切线,直线$CD$与$\odot O$相切于点$E$,则$AD· BC$的值为9。

答案：
15.9 [解析]本题考查切线的性质定理、切线长定理、相似三角形的判定与性质等知识.如图，连接OD、OC，$\because \odot O$的直径$AB=6$，$AD$、$BC$是它的两条切线，$\therefore AO=BO=\frac{1}{2}AB=3$，$AD\perp AB$于点A，$BC\perp AB$于点B，$\therefore AD// BC$，$\angle A=\angle B=90^{\circ}$，$\therefore \angle ADC+\angle BCD=180^{\circ}$.$\because$直线CD与$\odot O$相切于点E，$\therefore \angle ODC=\angle ODA=\frac{1}{2}\angle ADC$，
$\angle OCD=\angle OCB=\frac{1}{2}\angle BCD$，$\therefore \angle ODC+\angle OCD=\frac{1}{2}(\angle ADC+\angle BCD)=90^{\circ}$，$\therefore \angle DOC=180^{\circ}-(\angle ODC+\angle OCD)=90^{\circ}$，$\therefore \angle AOD=\angle BCO=90^{\circ}-\angle BOC$，$\therefore \triangle AOD\backsim \triangle BCO$，$\therefore \frac{AD}{BO}=\frac{AO}{BC}$，$\therefore AD· BC=AO· BO=9$.

知识拓展 切线的性质：①圆的切线垂直于经过切点的半径；②经过圆心且垂直于切线的直线必经过切点；③经过切点且垂直于切线的直线必经过圆心.运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直三角形解决有关问题.

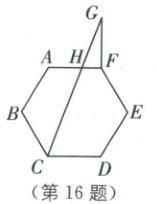
16.如图,已知正六边形$ABCDEF$,若将线段$AF$绕点$F$顺时针旋转$90^{\circ}$到$FG$,则$\frac{HG}{CH}$的值为$\frac{\sqrt{3}}{3}$。

答案：
16.$\frac{\sqrt{3}}{3}$ [解析]本题考查正多边形和圆、垂径定理、平行线分线段成比例定理以及勾股定理.如图，连接DF.$\because$六边形ABCDEF是正六边形，$\therefore \angle DEF=\frac{(6-2)× 180^{\circ}}{6}=120^{\circ}$，$\therefore \angle EDF=\angle EFD=\frac{180^{\circ}-120^{\circ}}{2}=30^{\circ}$.
$\therefore \angle CDF=120^{\circ}-30^{\circ}=90^{\circ}=\angle AFD$.又$\angle AFG=90^{\circ}$，D、F、G共线.设O为该六边形的外心，过点O作$OM\perp DF$于点M，则$DM=FM$.设正六边形ABCDEF的边长为a，则$OD=a$，$OM=\frac{1}{2}a$，
$\therefore DM=\sqrt{OD^{2}-OM^{2}}=\frac{\sqrt{3}}{2}a$，$\therefore DF=\sqrt{3}a$.$\because AF// CD$，
$\therefore \frac{GH}{CH}=\frac{FG}{DF}=\frac{a}{\sqrt{3}a}=\frac{\sqrt{3}}{3}$.

17.已知点$A(0,2a)$,$B(2,-2)$,若抛物线$y=ax^{2}-2ax-3a$与线段$AB$只有一个公共点,则$a$的取值范围为$0＜a\leqslant \frac{2}{3}$。

答案：
17.$0＜a\leqslant \frac{2}{3}$ [解析]本题考查了二次函数图像与系数的关系.根据题意求出抛物线的对称轴以及与x轴的交点坐标，然后分$a＞0$和$a＜0$两种情况讨论即可.
$\because y=ax^{2}-2ax-3a=a(x^{2}-2x-3)=a(x-3)(x+1)$，$\therefore$抛物线与x轴的交点为$(-1,0)$、$(3,0)$，对称轴为直线$x=\frac{-1+3}{2}=1$.
①当$a＞0$时，如图
(1).$\because$抛物线$y=ax^{2}-2ax-3a$与线段AB只有一个公共点，$\therefore$当$x=2$时，$-2\leqslant 4a-4a-3a＜0$，即$-2\leqslant -3a＜0$，解得$0＜a\leqslant \frac{2}{3}$；
②当$a＜0$时，如图
(2).此时抛物线与线段AB没有交点.
综上所述，$a$的取值范围为$0＜a\leqslant \frac{2}{3}$

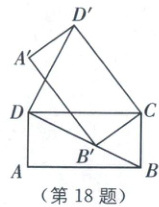
18.如图,已知矩形$ABCD$的边长$AB=8$,$BC=4$,若将矩形$ABCD$绕点$C$旋转,使点$B$的对应点$B'$恰好好落在$BD$上,连接$DD'$,则$DD'$的长为$\frac{16\sqrt{5}}{5}$。

答案：
18.$\frac{16\sqrt{5}}{5}$ [解析]本题考查矩形的性质、旋转的性质、等腰三角形的性质、相似三角形的判定与性质、勾股定理.如图，设$A^{\prime}B^{\prime}$交$DD^{\prime}$于点E，连接$B^{\prime}D^{\prime}$，作$CF\perp BD$于点F.
$\because$四边形ABCD是矩形，$BC=4$，$\therefore \angle A=90^{\circ}$，$AD=BC=4$，$\therefore BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{8^{2}+4^{2}}=4\sqrt{5}$.
由旋转得$B^{\prime}D^{\prime}=BD=4\sqrt{5}$，$B^{\prime}C=BC$，$\angle BCB^{\prime}=\angle DCD^{\prime}$，$\therefore \angle CB^{\prime}B=\angle CBB^{\prime}=\frac{1}{2}(180^{\circ}-\angle BCB^{\prime})=\frac{1}{2}(180^{\circ}-\angle DCD^{\prime})$，$CD^{\prime}D=\angle CDD^{\prime}=\frac{1}{2}(180^{\circ}-\angle DCD^{\prime})$，$\therefore \angle CB^{\prime}B=\angle CD^{\prime}D$.
$\because \angle A^{\prime}B^{\prime}C=\angle A^{\prime}D^{\prime}C=\angle A^{\prime}=90^{\circ}$，$\therefore \angle DB^{\prime}E+\angle CB^{\prime}B=90^{\circ}$，$\angle A^{\prime}D^{\prime}E+\angle CD^{\prime}D=90^{\circ}$，$\therefore \angle DB^{\prime}E=\angle A^{\prime}D^{\prime}E$，
$\therefore \angle B^{\prime}DD^{\prime}=\angle B^{\prime}ED^{\prime}-\angle DB^{\prime}E=\angle B^{\prime}ED^{\prime}-\angle A^{\prime}D^{\prime}E=\angle A^{\prime}=90^{\circ}$.
$\because \angle BFC=\angle BCD=90^{\circ}$，$\angle FBC=\angle CBD$，$\therefore \triangle BFC\backsim \triangle BCD$，$\therefore \frac{BF}{BC}=\frac{BC}{BD}$，$\therefore B^{\prime}F=BF=\frac{BC^{2}}{BD}=\frac{4^{2}}{4\sqrt{5}}=\frac{4\sqrt{5}}{5}$，
$\therefore DD^{\prime}=\sqrt{B^{\prime}D^{{\prime}2}-B^{\prime}D^{2}}=\sqrt{(4\sqrt{5})^{2}-(\frac{12\sqrt{5}}{5})^{2}}=\frac{16\sqrt{5}}{5}$.

19.(8 分)(1)计算:$\sin 30^{\circ}+\sqrt{2}\cos 45^{\circ}-\tan^{2}60^{\circ}$;
(2)解方程:$x+3=x^{2}+3x$.

答案： 19.[解析]本题考查了实数的运算和解一元二次方程.
(1)根据特殊角的三角函数值，代入计算即可；
(2)利用因式分解法解一元二次方程，即可得到答案.
解：$(1)\sin 30^{\circ}+\sqrt{2}\cos 45^{\circ}-\tan^{2}60^{\circ}=\frac{1}{2}+\sqrt{2}× \frac{\sqrt{2}}{2}-(\sqrt{3})^{2}=\frac{1}{2}+1-3=-\frac{3}{2}$.
(2)$\because x+3=x^{2}+3x$，$\therefore (x+3)(x-1)=0$，$\therefore x+3=0$或$x-1=0$，$\therefore x_{1}=-3$，$x_{2}=1$.

20.(8 分)已知关于$x$的一元二次方程$x^{2}-2(a+2)x+a^{2}-5=0$有实数根.
(1)求$a$的取值范围;
(2)若方程的两根为$x_{1}$、$x_{2}$,且$x_{1}^{2}+x_{2}^{2}=44$,求$a$的值.

答案： 20.[解析]本题考查了根与系数的关系及根的判别式.
(1)利用一元二次方程根的判别式即可解决问题；
(2)利用一元二次方程根与系数的关系即可解决问题.
解：$(1)\because$关于x的一元二次方程$x^{2}-2(a+2)x+a^{2}-5=0$有实数根，$\therefore \Delta =[-2(a+2)]^{2}-4(a^{2}-5)\geqslant 0$，解得$a\geqslant -\frac{9}{4}$，故a的取值范围是$a\geqslant -\frac{9}{4}$.
$(2)\because$方程的两根为$x_{1}$、$x_{2}$，$\therefore x_{1}+x_{2}=2a+4$，$x_{1}x_{2}=a^{2}-5$.$\because (x_{1}+x_{2})^{2}-2x_{1}x_{2}=44$，则$(2a+4)^{2}-2(a^{2}-5)=44$，解得$a=1$或$-9$.$\because a\geqslant -\frac{9}{4}$，
$\therefore a=1$.
知识拓展 一元二次方程$ax^{2}+bx+c=0(a\neq 0)$的根的判别式$\Delta =b^{2}-4ac$与根的关系：当$\Delta ＞0$时，一元二次方程有两个不相等的实数根；当$\Delta =0$时，一元二次方程有两个相等的实数根；当$\Delta ＜0$时，一元二次方程没有实数根.