第115页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
1.(2025·广东广州花都区黄广中学期中)我国南宋数学家杨辉在1275年提出的一个问题:“直田积八百六十四步,只云阔不及长一十二步.问阔及长各几步.”意思是:长方形的面积是864平方步,宽比长少12步.问宽和长各是几步.设宽为$x$步,根据题意列方程正确的是(
A.$2x+2(x+12)=864$
B.$x^{2}+(x+12)^{2}=864$
C.$x(x-12)=864$
D.$x(x+12)=864$
D
).A.$2x+2(x+12)=864$
B.$x^{2}+(x+12)^{2}=864$
C.$x(x-12)=864$
D.$x(x+12)=864$
答案:
1.D [解析]设宽为x步,则长为(x+12)步.根据题意列方程x(x+12)=864.故选D.
2.(2024·深圳中考)二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律,二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨),夏季(立夏、小满、芒种、夏至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小寒、大寒),若从二十四个节气中选一个节气,则抽到的节气在夏季的概率为(
A.$\frac{1}{2}$
B.$\frac{1}{12}$
C.$\frac{1}{6}$
D.$\frac{1}{4}$
D
).A.$\frac{1}{2}$
B.$\frac{1}{12}$
C.$\frac{1}{6}$
D.$\frac{1}{4}$
答案:
2.D [解析]从二十四个节气中选一个节气,则抽到的节气在夏季的概率为$\frac{6}{24}=\frac{1}{4}$.故选D.
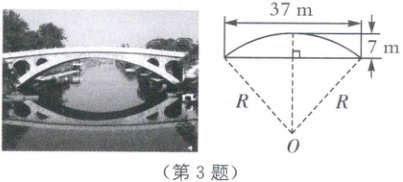
3.拱桥模型(2024·南京科利华中学三模)赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为$37 m$,拱高约为$7 m$,则赵州桥主桥拱半径$R$约为(
A.$20 m$
B.$28 m$
C.$35 m$
D.$40 m$
B
).
A.$20 m$
B.$28 m$
C.$35 m$
D.$40 m$
答案:
3.B [解析]如图,$AB = 37m$,$CD = 7m$,设主桥拱半径为$R$,$\therefore OD = OC - CD = (R - 7)m$.
$\because OC$是半径,$OC\perp AB$,$\therefore AD = BD = \frac{1}{2}AB = \frac{37}{2}(m)$.
在$Rt\triangle ADO$中,$AD^{2} + OD^{2} = OA^{2}$,
$\therefore (\frac{37}{2})^{2} + (R - 7)^{2} = R^{2}$,解得$R = \frac{1565}{56} \approx 28(m)$.
故选B.

3.B [解析]如图,$AB = 37m$,$CD = 7m$,设主桥拱半径为$R$,$\therefore OD = OC - CD = (R - 7)m$.
$\because OC$是半径,$OC\perp AB$,$\therefore AD = BD = \frac{1}{2}AB = \frac{37}{2}(m)$.
在$Rt\triangle ADO$中,$AD^{2} + OD^{2} = OA^{2}$,
$\therefore (\frac{37}{2})^{2} + (R - 7)^{2} = R^{2}$,解得$R = \frac{1565}{56} \approx 28(m)$.
故选B.

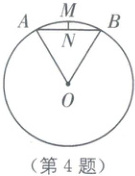
4.(2023·宜宾中考)《梦溪笔谈》是我国古代科技著作,其中它记录了计算圆弧长度的“会圆术”.如图,$\overset{\frown} {AB}$是以点$O$为圆心、$OA$为半径的圆弧,$N$是$AB$的中点,$MN\perp AB$.“会圆术”给出$\overset{\frown} {AB}$的弧长$l$的近似值计算公式:$l=AB+\frac{MN^{2}}{OA}$.当$OA=4$,$\angle AOB=60^{\circ }$时,则$l$的值为(
A.$11 - 2\sqrt{3}$
B.$11 - 4\sqrt{3}$
C.$8 - 2\sqrt{3}$
D.$8 - 4\sqrt{3}$
B
).
A.$11 - 2\sqrt{3}$
B.$11 - 4\sqrt{3}$
C.$8 - 2\sqrt{3}$
D.$8 - 4\sqrt{3}$
答案:
4.B [解析]连接$ON$,如图.
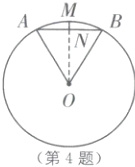
$\because \overgroup{AB}$是以$O$为圆心,$OA$为半径的圆弧,$N$是$AB$的中点,$MN\perp AB$,$\therefore ON\perp AB$,$\therefore M$、$N$、$O$共线.
$\because OA = 4$,$\angle AOB = 60^{\circ}$,$\therefore \triangle AOB$是等边三角形,
$\therefore OA = AB = 4$,$\angle OAN = 60^{\circ}$,
$\therefore ON = OA· \sin60^{\circ} = 2\sqrt{3}$,
$\therefore MN = OM - ON = 4 - 2\sqrt{3}$,
$\therefore l = AB + \frac{MN^{2}}{OA} = 4 + \frac{(4 - 2\sqrt{3})^{2}}{4} = 11 - 4\sqrt{3}$.故选B.
思路引导 解题的关键是读懂题意,作出辅助线求$ON$的长度后代入弧长$l$的近似值计算公式.
4.B [解析]连接$ON$,如图.

$\because \overgroup{AB}$是以$O$为圆心,$OA$为半径的圆弧,$N$是$AB$的中点,$MN\perp AB$,$\therefore ON\perp AB$,$\therefore M$、$N$、$O$共线.
$\because OA = 4$,$\angle AOB = 60^{\circ}$,$\therefore \triangle AOB$是等边三角形,
$\therefore OA = AB = 4$,$\angle OAN = 60^{\circ}$,
$\therefore ON = OA· \sin60^{\circ} = 2\sqrt{3}$,
$\therefore MN = OM - ON = 4 - 2\sqrt{3}$,
$\therefore l = AB + \frac{MN^{2}}{OA} = 4 + \frac{(4 - 2\sqrt{3})^{2}}{4} = 11 - 4\sqrt{3}$.故选B.
思路引导 解题的关键是读懂题意,作出辅助线求$ON$的长度后代入弧长$l$的近似值计算公式.
5.(2025·吕梁方山一模)晋剧是我省国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱,正面印有晋剧经典剧目Q版人物的三张卡片(其中有1名男性角色,2名女性角色),它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面人物性别都为女性的概率为(
A.$\frac{2}{3}$
B.$\frac{1}{3}$
C.$\frac{5}{9}$
D.$\frac{4}{9}$
D
).A.$\frac{2}{3}$
B.$\frac{1}{3}$
C.$\frac{5}{9}$
D.$\frac{4}{9}$
答案:
5.D [解析]1名男性角色记为$A$,2名女性角色分别记为$B$、$C$,画树状图如下:
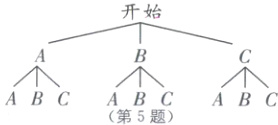
由图可知,共有9种等可能的结果,其中$B$、$B$;$B$、$C$;$C$、$B$;$C$、$C$四种结果为女性,$\therefore$两次抽取的卡片正面人物性别都为女性的概率为$\frac{4}{9}$.故选D.
5.D [解析]1名男性角色记为$A$,2名女性角色分别记为$B$、$C$,画树状图如下:

由图可知,共有9种等可能的结果,其中$B$、$B$;$B$、$C$;$C$、$B$;$C$、$C$四种结果为女性,$\therefore$两次抽取的卡片正面人物性别都为女性的概率为$\frac{4}{9}$.故选D.
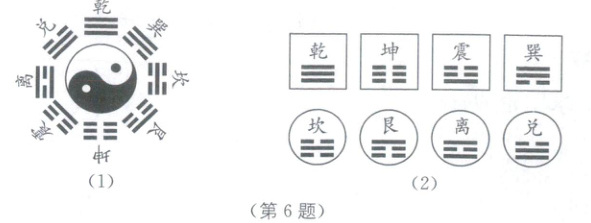
6.(2025·郑州金水区一模)八卦图是中国古老的科学文化遗产,是我国古代劳动人民智慧的结晶.如图(1)所示的八卦图中每一卦由“—”和“--”组成.小明制作了如图(2)所示的4张方形卡片和4张圆形卡片(方形卡片、圆形卡片的背面均相同),4张方形卡片上分别画有乾、坤、震、巽四卦,4张圆形卡片上分别画有坎、艮、离、兑四卦.小明将这些卡片背面朝上洗匀,并从方形卡片中随机抽取一张,从圆形卡片中随机抽取一张,则抽到的两张卡片上的卦中都只有1根“—”的概率是(
A.$\frac{1}{8}$
B.$\frac{1}{2}$
C.$\frac{3}{8}$
D.$\frac{5}{8}$
A
).
A.$\frac{1}{8}$
B.$\frac{1}{2}$
C.$\frac{3}{8}$
D.$\frac{5}{8}$
答案:
6.A [解析]解法一:根据题意方形卡片中震符合题意,圆形卡片中坎、艮符合题意,列表如下:
总共有16种等可能的情况,每种情况出现的可能性相同,符合情况的有2种,则抽到的两张卡片上的卦中都只有1根“—”的概率为$\frac{2}{16}=\frac{1}{8}$.故选A.
一题多解 根据图意方形卡片中震符合题意,圆形卡片中坎、艮符合题意,画树状图如图:
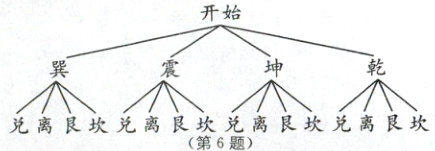
总共有16种等可能的情况,每种情况出现的可能性相同,符合情况的有2种,则抽到的两张卡片上的卦中都只有1根“—”的概率为$\frac{2}{16}=\frac{1}{8}$.
6.A [解析]解法一:根据题意方形卡片中震符合题意,圆形卡片中坎、艮符合题意,列表如下:
总共有16种等可能的情况,每种情况出现的可能性相同,符合情况的有2种,则抽到的两张卡片上的卦中都只有1根“—”的概率为$\frac{2}{16}=\frac{1}{8}$.故选A.
一题多解 根据图意方形卡片中震符合题意,圆形卡片中坎、艮符合题意,画树状图如图:

总共有16种等可能的情况,每种情况出现的可能性相同,符合情况的有2种,则抽到的两张卡片上的卦中都只有1根“—”的概率为$\frac{2}{16}=\frac{1}{8}$.
查看更多完整答案,请扫码查看


