《2025年实验班提优大考卷九年级数学上册苏科版》

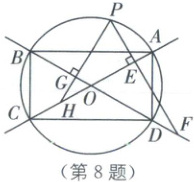
8. 数形结合思想 (2025·无锡梁溪区一模)如图,在$\bigodot O$中,$AC, BD$是直径,$\angle BOC = 60°$,点$P$是劣弧$AB$上任意一点(不与$A, B$重合),过点$P$作$AC$的垂线,交$AC, BD$所在直线于点$E, F$,过点$P$作$BD$的垂线,交$BD, AC$所在直线于点$G, H$,下列选项中,正确的是(B).
① $\frac{PE}{PG} = \frac{PH}{PF}$;
② $\angle GPE = 60°$;
③ $PG + PE$最大值为$\frac{3\sqrt{3}}{2} AO$;
④ 当$\triangle PEH \cong \triangle CBA$时,$S_{\triangle PGF}: S_{ 矩形ABCD} = 1:8$.

A.①②③
B.①②④
C.①③④
D.①②③④

答案：
8.B [解析]①
∵PG⊥BD，PE⊥AC，
∴∠PEH=∠PGF=90°.
∵∠HPE=∠FPG，
∴△PEH∽△PGF.
∴$\frac{PE}{PG}$=$\frac{PH}{PF}$.故①正确；②
∵∠BOC=60°，
∴∠GOE=180°－∠BOC=120°.
∵PG⊥BD，PE⊥AC，
∴∠PGO=∠PEO=90°.在四边形PGOE中，∠GPE=360°－(∠PGO+∠PEO+∠GOE)=60°.故②正确；③连接PA、PB、PO，过点P作PM⊥AB于M，如图
(1)，
∵S△POB+S△POA=S△AOB+S△PAB，且AC，BD是⊙O直径，∠AOB=120°，
∴OA=OB为定值，S△AOB为定值.
∴$\frac{1}{2}$OB·PG+$\frac{1}{2}$OA·PE=S△AOB+$\frac{1}{2}$AB·PM.
∴PG+PE=$\frac{2S_{\triangle AOB}}{OA}$+$\frac{AB}{OA}$·PM.
∴$\frac{2S_{\triangle AOB}}{OA}$+$\frac{AB}{OA}$为定值，
∴当PM最大时，PG+PE最大.
∵点P是劣弧AB上任意一点(不与A、B重合)，
∴当点P是劣弧AB的中点时，PM最大，此时PG+PE最大，且O、P、M三点共线，如图
(2).
∵点M在线段PO上，且PO⊥AB，PA=PB.
∴∠AOP=$\frac{1}{2}$∠AOB=60°.在Rt△OAM中，∠OAM=90°－∠AOP=30°，
∴OM=$\frac{1}{2}$OA=$\frac{1}{2}$OP，则PM=$\frac{1}{2}$OA.由勾股定理，得AM=$\sqrt{OA^{2}-OM^{2}}$=$\frac{\sqrt{3}}{2}$OA，
∴AB=2AM=$\sqrt{3}$OA.
∴S△AOB=$\frac{1}{2}$AB·OM=$\frac{1}{2}$×$\sqrt{3}$OA×$\frac{1}{2}$OA=$\frac{\sqrt{3}}{4}$$OA^{2}$，
∴PG+PE的最大值为$\frac{2×\frac{\sqrt{3}}{4}OA^{2}}{OA}$+$\frac{\sqrt{3}OA}{OA}$·PM=$\frac{2×\frac{\sqrt{3}}{4}OA^{2}}{OA}$+$\frac{\sqrt{3}OA}{OA}$×$\frac{1}{2}$OA=$\sqrt{3}OA$×$\frac{1}{2}$OA=$\sqrt{3}OA$.故③不正确；④当△PEH≌△CBA时，则PE=BC.
∵OB=OC，∠BOC=60°，
∴△OBC为等边三角形.
∴OB=BC=OP，此时点E、F均与点O重合，如图
(3)，
∵AC=BD，OA=OB=OC=OD，
∴四边形ABCD为矩形.
∴∠BAC=$\frac{1}{2}$∠BOC=30°.
∴AC=2BO=2OA.由勾股定理，得AB=$\sqrt{AC^{2}-BC^{2}}$=$\sqrt{3}$OA，
∴S矩形ABCD=AB·BC=$\sqrt{3}$OA·OA=$\sqrt{3}$$OA^{2}$.在Rt△OPG中，∠GOP=∠AOB－∠POA=120°－90°=30°，
∴PG=$\frac{1}{2}$OP=$\frac{1}{2}$OA.由勾股定理，得OG=$\sqrt{OP^{2}-PG^{2}}$=$\frac{\sqrt{3}}{2}$OA，
∴S△PGF=$\frac{1}{2}$PG·OG=$\frac{1}{2}$×$\frac{1}{2}$OA×$\frac{\sqrt{3}}{2}$OA=$\frac{\sqrt{3}}{8}$$OA^{2}$.
∴S△PGF:S矩形ABCD=1:8.故④正确.综上所述，正确的是①②④.故选B.

9. 转化思想 若$\frac{x}{6} = \frac{y}{4} = \frac{z}{3}$($x, y, z$均不为0),则$\frac{x + 3y}{3y - 2z} =$ 3.

答案： 9.3 [解析]设$\frac{x}{6}$=$\frac{y}{4}$=$\frac{z}{3}$=k(k≠0)，则x=6k，y=4k，z=3k，所以$\frac{x+3y}{3y-2z}$=$\frac{6k+12k}{12k-6k}$=3.

10. 已知线段$a = 4 cm$,$b = 9 cm$,且线段$a$是线段$b$和线段$c$的比例中项,则线段$c$的长是$\frac{16}{9}$cm .

答案： 10.$\frac{16}{9}$cm [解析]
∵线段a是线段b、c的比例中项，
∴$a^{2}$=bc.
∵a=4cm，b=9cm，
∴$4^{2}$=9c，
∴c=$\frac{16}{9}$cm.

11. 传统文化 古筝 (2025·浙江华东师大附属学校期中)如图,乐器上的一根弦$AB = 80 cm$,两个端点$A, B$固定在乐器面板上,支撑点$C$是靠近点$B$的黄金分割点,支撑点$D$是靠近点$A$的黄金分割点,则支撑点$C, D$之间的距离为(80$\sqrt{5}$－160) $ cm$.(结果保留根号)

答案： 11.(80$\sqrt{5}$－160) [解析]
∵点C是靠近点B的黄金分割点，AB=80cm，
∴AC=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$×80=(40$\sqrt{5}$－40)cm.
∵点D是靠近点A的黄金分割点，AB=80cm，
∴DB=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$×80=(40$\sqrt{5}$－40)cm，
∴CD=AC+BD－AB=2(40$\sqrt{5}$－40)－80=(80$\sqrt{5}$－160)cm，
∴支撑点C、D之间的距离为(80$\sqrt{5}$－160)cm.

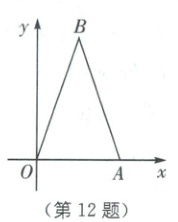
12. 如图,$\triangle AOB$三个顶点的坐标分别为$A(4,0), O(0,0), B(2,6)$,以点$O$为位似中心,将$\triangle AOB$在第一象限缩小,若点$B$的对应点$B'$的坐标$(1,3)$,则$\frac{S_{\triangle A'O'B'}}{S_{\triangle AOB}}$的比值为$\frac{1}{4}$.

答案： 12.$\frac{1}{4}$ [解析]
∵以点O为位似中心，将△AOB在第一象限缩小，点B的坐标为(2，6)，点B的对应点B'的坐标(1，3)，
∴△A'OB'与△AOB的相似比为$\frac{1}{2}$，
∴$\frac{S_{\triangle A'OB'}}{S_{\triangle AOB}}$=$\frac{1}{4}$.

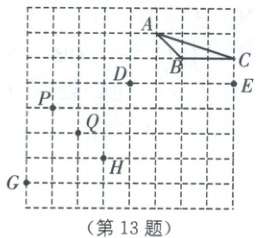
13. 图中的每个点(包括$\triangle ABC$的各个顶点)都在边长为1的小正方形的顶点上,在$P, Q, G, H$中找一个点,使它与点$D, E$构成的三角形与$\triangle ABC$相似,这个点可以是Q或G. (写出满足条件的所有的点)

答案： 13.Q或G [解析]这个点是点Q或点G，根据两边成比例夹角相等即可判断.

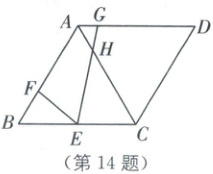
14. (2025·徐州十三中期末)如图,在菱形$ABCD$中,$\angle B = 60°$,$BC = 6$,$E$为$BC$的中点,$F$是$AB$上一点,$G$为$AD$上一点,且$BF = 2$,$\angle FEG = 60°$,$EG$交$AC$于点$H$,则$\frac{S_{\triangle BEF}}{S_{\triangle AGH}}$的值为4.

答案： 14.4 [解析]在菱形ABCD中，∠B=60°，BC=6，E为BC的中点，∠FEG=60°，
∴∠B=∠ECH=60°，∠BEF=∠CHE=120°－∠CEH.
∴△BEF∽△CHE.
∴$\frac{BF}{CE}$=$\frac{BE}{CH}$
∵CE=BE=3，BF=2，
∴$\frac{2}{3}$=$\frac{3}{CH}$，解得CH=4.5.
∵AC=BC=6，
∴AH=1.5.
∵AG//CE，
∴△AGH∽△CEH.
∴$\frac{AG}{CE}$=$\frac{AH}{CH}$=$\frac{1}{3}$，
∴AG=$\frac{1}{3}$CE=1.
∵BF=$\frac{2}{3}$CE，△BEF∽△CHE，△AGH∽△CEH，
∴S△CEH=9S△AGH，S△CEH=$\frac{9}{4}$S△BEF.
∴9S△AGH=$\frac{9}{4}$S△BEF，
∴S△BEF=4S△AGH，
∴$\frac{S_{\triangle BEF}}{S_{\triangle AGH}}$=4.

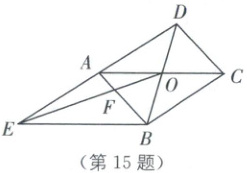
15. (2023·抚顺中考)如图,平行四边形$ABCD$的对角线$AC, BD$相交于点$O$,过点$B$作$BE // AC$,交$DA$的延长线于点$E$,连接$OE$,交$AB$于点$F$,则四边形$BCOF$的面积与$\triangle AEF$的面积的比值为$\frac{5}{2}$.

答案： 15.$\frac{5}{2}$ [解析]
∵四边形ABCD是平行四边形，
∴AD//BC，OA=OC.又BE//AC，
∴四边形AEBC是平行四边形，
∴AC=BE，
∴BE=2OA.
∵BE//AC，
∴△OAF∽△EBF，
∴$\frac{S_{\triangle OAF}}{S_{\triangle EBF}}$=$(\frac{OA}{BE})^{2}$=$(\frac{1}{2})^{2}$=$\frac{1}{4}$，
∴S△EBF=4S△OAF，$\frac{S_{\triangle AFE}}{S_{\triangle AOF}}$=$\frac{EF}{OF}$=2，
∴S△AEF=2S△AOF.同理S△EBF=2S△OBF，S△OBC=S△OAB.设S△OAF=x，则S△EBF=4x，S△AEF=2x，S△OBF=2x，
∴S△AOB=S△AOF+S△BOF=x+2x=3x，S四边形BCOF=S△BOC+S△BOF=3x+2x=5x，
∴$\frac{S_{四边形BCOF}}{S_{\triangle AEF}}$=$\frac{5x}{2x}$=$\frac{5}{2}$.

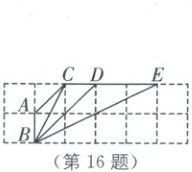
16. 如图,在正方形网格中有三个三角形,分别是$\triangle EBC, \triangle CDB, \triangle DEB$,其中与$\triangle ABC$相似的是△DEB.

答案： 16.△DEB [解析]
∵△ABC的三边之比是AB:AC:BC=1:$\sqrt{2}$:$\sqrt{5}$，△EBC的三边之比是BC:EC:BE=$\sqrt{5}$:3:2$\sqrt{5}$；△CDB的三边之比是CD:BC:BD=1:$\sqrt{5}$:2$\sqrt{2}$；△DEB的三边之比是DE:BD:BE=2:2$\sqrt{2}$:$\sqrt{20}$=1:$\sqrt{2}$:$\sqrt{5}$，
∴△DEB与△ABC相似.

17. (2023·绥化中考)如图,在平面直角坐标系中,$\triangle ABC$与$\triangle AB'C'$的相似比为$1:2$,点$A$是位似中心,已知点$A(2,0)$,点$C(a,b)$,$\angle C = 90°$,则点$C'$的坐标为(6－2a，－2b) .(结果用含$a, b$的式子表示)

答案：
17.(6－2a，－2b) [解析]如图，过点C作CM⊥AB于点M，过点C'作C'N⊥AB'于点N，则∠ANC'=∠AMC=90°.
∵△ABC与△AB'C'的相似比为1:2，
∴$\frac{AC}{AC'}$=$\frac{1}{2}$.
∵∠NAC'=∠CAM，
∴△ACM∽△AC'N，
∴$\frac{AM}{AN}$=$\frac{CM}{C'N}$=$\frac{AC}{AC'}$.
∵点A(2，0)，点C(a，b)，
∴OA=2，OM=a，CM=b，
∴AM=a－2，
∴$\frac{a-2}{AN}$=$\frac{b}{C'N}$=$\frac{1}{2}$，
∴AN=2a－4，C'N=2b，
∴ON=AN－OA=2a－6，
∴点C'的坐标为(6－2a，－2b).