第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
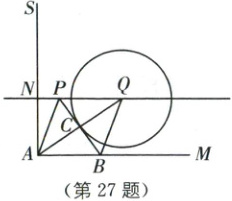
27. (10 分)(2025·无锡新吴区期中)已知线段 AM=5,射线 AS 垂直于 AM,点 N 在射线 AS 上,设 AN=n,点 P 在经过点 N 且平行于 AM 的直线上运动,∠PAM 的平分线交直线 NP 于点 Q,过点 Q 作 QB//AP,交线段 AM 于点 B,连接 PB 交 AQ 于点 C,以 Q 为圆心,QC 为半径作圆.
(1)判断 PB 与⊙Q 的位置关系:
(2)已知⊙Q 的半径为 3,当 AM 所在直线与⊙Q 相切时,求 PA 的长.
(3)当 n=2 时,若⊙Q 与线段 AM 只有一个公共点,则⊙Q 的半径的取值范围是多少?
(1)判断 PB 与⊙Q 的位置关系:
相切
.(2)已知⊙Q 的半径为 3,当 AM 所在直线与⊙Q 相切时,求 PA 的长.
(3)当 n=2 时,若⊙Q 与线段 AM 只有一个公共点,则⊙Q 的半径的取值范围是多少?

答案:
27.
(1)相切 [解析]
∵∠PAM的平分线交直线NP于点Q,
∴∠PAQ=∠BAQ.
∵PQ//AB,
∴∠PQA=∠BAQ,
∴∠PAQ=∠PQA,
∴PA=PQ.
又QB//PA,
∴四边形APQB为平行四边形,
∴四边形APQB为菱形,
∴PB⊥AQ,垂足为C.
∵QC为半径,
∴PB与⊙Q相切.
(2)如图
(1),当AM与⊙Q相切于点D时,AN=QD=QC=3,∠ADQ=90°.由
(1),得四边形APQB为菱形,
∴AQ=6.
在Rt△ADQ中,AD=$\sqrt{AQ²−QD²}$=3$\sqrt{3}$.
设AP=AB=BQ=x,则BD=3$\sqrt{3}$−x,
在Rt△BDQ中,(3$\sqrt{3}$−x)²+3²=x²,
解得x=2$\sqrt{3}$,
∴PA=2$\sqrt{3}$.



(3)如图
(1),当⊙Q与AM相切时,r=2,此时⊙Q与AM只有一个公共点.
当⊙Q过点M时,如图
(2),连接QM,作QE⊥AM于点E,则QM=QC=x,则AQ=2x,由NQ+ME=AM=5,
得$\sqrt{(2x)²−2²}$+$\sqrt{x²−2²}$=5.
设x²=y,则方程转化为9y²−250y+1025=0,
方程中出现根号时可利用换元法消去
根号来简化方程,使解题更快
解得y₁=5,y₂=$\frac{205}{9}$,
∴x₁=$\sqrt{5}$,x₂=$\frac{\sqrt{205}}{3}$(舍去).
当⊙Q第二次经过点M时,作ME⊥NQ于点E,如图
(3),设QM=QC=x,则AQ=2x,由NQ−EQ=
AM=5,得$\sqrt{(2x)²−2²}$−$\sqrt{x²−2²}$=5.
设x²=y,则方程转化为9y²−250y+1025=0,
解得y₁=5,y₂=$\frac{205}{9}$,
∴x₁=$\sqrt{5}$,x₂=$\frac{\sqrt{205}}{3}$(舍去),
∴⊙Q与线段AM只有一个公共点,则⊙Q的半径的取值范围是QC=2或$\sqrt{5}$<QC≤$\frac{\sqrt{205}}{3}$.
27.
(1)相切 [解析]
∵∠PAM的平分线交直线NP于点Q,
∴∠PAQ=∠BAQ.
∵PQ//AB,
∴∠PQA=∠BAQ,
∴∠PAQ=∠PQA,
∴PA=PQ.
又QB//PA,
∴四边形APQB为平行四边形,
∴四边形APQB为菱形,
∴PB⊥AQ,垂足为C.
∵QC为半径,
∴PB与⊙Q相切.
(2)如图
(1),当AM与⊙Q相切于点D时,AN=QD=QC=3,∠ADQ=90°.由
(1),得四边形APQB为菱形,
∴AQ=6.
在Rt△ADQ中,AD=$\sqrt{AQ²−QD²}$=3$\sqrt{3}$.
设AP=AB=BQ=x,则BD=3$\sqrt{3}$−x,
在Rt△BDQ中,(3$\sqrt{3}$−x)²+3²=x²,
解得x=2$\sqrt{3}$,
∴PA=2$\sqrt{3}$.



(3)如图
(1),当⊙Q与AM相切时,r=2,此时⊙Q与AM只有一个公共点.
当⊙Q过点M时,如图
(2),连接QM,作QE⊥AM于点E,则QM=QC=x,则AQ=2x,由NQ+ME=AM=5,
得$\sqrt{(2x)²−2²}$+$\sqrt{x²−2²}$=5.
设x²=y,则方程转化为9y²−250y+1025=0,
方程中出现根号时可利用换元法消去
根号来简化方程,使解题更快
解得y₁=5,y₂=$\frac{205}{9}$,
∴x₁=$\sqrt{5}$,x₂=$\frac{\sqrt{205}}{3}$(舍去).
当⊙Q第二次经过点M时,作ME⊥NQ于点E,如图
(3),设QM=QC=x,则AQ=2x,由NQ−EQ=
AM=5,得$\sqrt{(2x)²−2²}$−$\sqrt{x²−2²}$=5.
设x²=y,则方程转化为9y²−250y+1025=0,
解得y₁=5,y₂=$\frac{205}{9}$,
∴x₁=$\sqrt{5}$,x₂=$\frac{\sqrt{205}}{3}$(舍去),
∴⊙Q与线段AM只有一个公共点,则⊙Q的半径的取值范围是QC=2或$\sqrt{5}$<QC≤$\frac{\sqrt{205}}{3}$.
28. (10 分)中考新考法 操作探究 如图,在平面直角坐标系 xOy 中,已知点 A(6,0)、B(0,6),动点 C 在以 3 为半径的⊙O 上,连接 OC,过点 O 作 OD⊥OC,OD 与⊙O 相交于点 D(其中点 C、O、D 按逆时针方向排列),连接 AB.
(1)当 OC//AB 时,∠BOC 的度数为
(2)连接 AC、BC,当点 C 在⊙O 上运动到什么位置时,△ABC 的面积最大? 并求出△ABC 的面积的最大值.
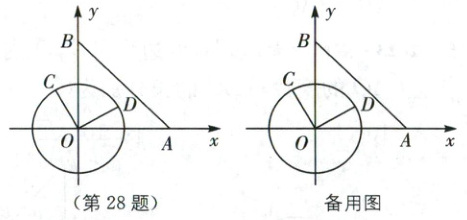
(3)连接 AD,当 OC//AD 时.
①求点 C 的坐标.
②直线 BC 是否为⊙O 的切线? 请作出判断,并说明理由.
(1)当 OC//AB 时,∠BOC 的度数为
45°或135°
.(2)连接 AC、BC,当点 C 在⊙O 上运动到什么位置时,△ABC 的面积最大? 并求出△ABC 的面积的最大值.

(3)连接 AD,当 OC//AD 时.
①求点 C 的坐标.
②直线 BC 是否为⊙O 的切线? 请作出判断,并说明理由.
答案:
28.
(1)45°或135°
(2)当CO的延长线与AB垂直时(如图
(1)所示),△ABC的面积最大.设CO的延长线交AB于点E.
由题意,得OA=OB=6,AB=6$\sqrt{2}$.
又OE⊥AB,
∴OE=3$\sqrt{2}$.
又OC=3,
∴CE=3+3$\sqrt{2}$,
∴S△ABC的最大值=$\frac{1}{2}$AB·CE=$\frac{1}{2}$×6$\sqrt{2}$×(3+3$\sqrt{2}$)=18+9$\sqrt{2}$.
(3)①如图
(2),连接AD,过点C作CF⊥x轴,垂足为F.
∵OC//AD,OC⊥OD,
∴OD⊥AD,
∴∠ADO=90°.
又OD=3,AO=6,
∴∠AOD=60°,
∴∠COF=30°.
又OC=3,
∴OF=$\frac{3\sqrt{3}}{2}$,CF=$\frac{3}{2}$,
∴C(−$\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$).
②直线BC是⊙O的切线.理由如下:
如图
(2),连接BC.
∵∠AOD+∠DOB=90°,∠COB+∠DOB=90°,
∴∠AOD=∠BOC.
在△AOD和△BOC中,$\begin{cases}AO=BO,\\\angle AOD=\angle BOC,\\OD=OC.\end{cases}$
∴△AOD≌△BOC(SAS),
∴∠ADO=∠BCO.
由①,可知∠ADO=90°,
∴∠BCO=90°,即OC⊥BC.又OC为⊙O半径.
故直线BC为⊙O的切线.

28.
(1)45°或135°
(2)当CO的延长线与AB垂直时(如图
(1)所示),△ABC的面积最大.设CO的延长线交AB于点E.
由题意,得OA=OB=6,AB=6$\sqrt{2}$.
又OE⊥AB,
∴OE=3$\sqrt{2}$.
又OC=3,
∴CE=3+3$\sqrt{2}$,
∴S△ABC的最大值=$\frac{1}{2}$AB·CE=$\frac{1}{2}$×6$\sqrt{2}$×(3+3$\sqrt{2}$)=18+9$\sqrt{2}$.
(3)①如图
(2),连接AD,过点C作CF⊥x轴,垂足为F.
∵OC//AD,OC⊥OD,
∴OD⊥AD,
∴∠ADO=90°.
又OD=3,AO=6,
∴∠AOD=60°,
∴∠COF=30°.
又OC=3,
∴OF=$\frac{3\sqrt{3}}{2}$,CF=$\frac{3}{2}$,
∴C(−$\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$).
②直线BC是⊙O的切线.理由如下:
如图
(2),连接BC.
∵∠AOD+∠DOB=90°,∠COB+∠DOB=90°,
∴∠AOD=∠BOC.
在△AOD和△BOC中,$\begin{cases}AO=BO,\\\angle AOD=\angle BOC,\\OD=OC.\end{cases}$
∴△AOD≌△BOC(SAS),
∴∠ADO=∠BCO.
由①,可知∠ADO=90°,
∴∠BCO=90°,即OC⊥BC.又OC为⊙O半径.
故直线BC为⊙O的切线.

查看更多完整答案,请扫码查看


