《2025年实验班提优大考卷九年级数学上册苏科版》

8. (2025·河北廊坊霸州期末)已知点$ P(m - 2, n) $,$ Q(m + 1, n) $,$ M(m + 3, n) $,$ N(m + 2, n - 2) $,二次函数的图象经过这四个点中的三个点,得到对应的函数解析式为$ y = ax^2 + bx + c $,当$ a $的值最大时,所对应的二次函数图象经过的点为(D).

A.点$ P $,点$ Q $和点$ M $
B.点$ P $,点$ Q $和点$ N $
C.点$ P $,点$ M $和点$ N $
D.点$ Q $,点$ M $和点$ N $

答案：
8.D　[解析]建立平面直角坐标系，四个点的大致位置如图，

∵P(m - 2,n)、Q(m + 1,n)、M(m + 3,n)在一条直线上，故A不符合题意；
由题意可知该二次函数的图像必过点N(m + 2,n - 2)，且过点P(m - 2,n)、Q(m + 1,n)、M(m + 3,n)中的任意2个点，当抛物线过P、Q、N三点时开口向下，此时a＜0；
当抛物线过P、M、N或Q、M、N三点时开口向上，此时a＞0，故B不符合题意；
∵当a＞0时，开口越小a越大，
由图可知，过Q、M、N三点的二次函数图像的开口更小，
∴过Q、M、N三点时a最大，故D符合题意.故选D.

9. 已知函数$ y = (k + 2)x^{k^2 + k - 4} $是关于$ x $的二次函数,则$ k = $2或 - 3.

答案： 9.2或 - 3　[解析]
∵函数$y = (k + 2)x^{k² + k - 4}$是关于x的二次函数，
∴k² + k - 4 = 2，且k + 2≠0，解得k = 2或 - 3.

10. 把二次函数$ y = x^2 - 4x + 5 $化为$ y = a(x - h)^2 + k $的形式,则$ h + k = $3.

答案： 10.3　[解析]
∵y = x² - 4x + 5 = (x - 2)² + 1，
∴h = 2，k = 1，
∴h + k = 2 + 1 = 3.

11. (2023·牡丹江中考)将抛物线$ y = (x + 3)^2 $向下平移1个单位长度,再向右平移2或4个单位长度后,得到的新抛物线经过原点.

答案： 11.2或4　[解析]抛物线y = (x + 3)²向下平移1个单位长度的表达式为y = (x + 3)² - 1，设抛物线向右平移h个单位长度后，得到的新抛物线经过原点，则新抛物线的表达式为y = (x + 3 - h)² - 1.
∵抛物线经过原点，
∴当x = 0时，y = 0，
∴(3 - h)² - 1 = 0，解得h = 2或4.

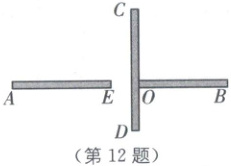
12. (2024·自贡中考)九(1)班劳动实践基地内有一块面积足够大的平整空地,地上两段围墙$ AB \perp CD $于点$ O $(如图),其中$ AB $上的$ EO $段围墙空缺.同学们测得$ AE = 6.6 \, m $,$ OE = 1.4 \, m $,$ OB = 6 \, m $,$ OC = 5 \, m $,$ OD = 3 \, m $,班长买来可切断的围栏16 m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是46.4$ m^2 $.

答案： 12.46.4　[解析]设矩形在射线OA上的一段长为xm.
(1)当x≤8时，S = x·$\frac{16 - x - 1.4 + 5}{2}$ = -$\frac{1}{2}$x² + 9.8x = -$\frac{1}{2}$(x - 9.8)² + 48.02，
当x = 8时，S = 46.4.
(2)当x＞8时，S = x·($\frac{16 + 6.6 + 5}{2}$ - x) = -x² + 13.8x = -(x - 6.9)² + 47.61，
由于在x＞8的范围内，S均小于46.4.
所以由
(1)
(2)得最大面积为46.4m².

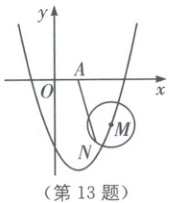
13. (2024·浙江嘉兴平湖期末)如图,已知点$ M(a, b)(b ＜ 0) $为抛物线$ y = x^2 - 2x - 3 $上的动点,点$ N $是以点$ M $为圆心,1为半径的圆上的动点,点$ A(1, 0) $,则线段$ AN $的最小值为$\frac{\sqrt{15}}{2}$ - 1.

答案：
13.$\frac{\sqrt{15}}{2}$ - 1　[解析]连接AM、MN，如图所示.

∵点M(a,b)在抛物线y = x² - 2x - 3上，
∴b = a² - 2a - 3.
∴b + 3 = a² - 2a.
∵点A(1,0)，
∴AM² = (a - 1)² + b² = a² - 2a + 1 + b² = b² + b + 4 = (b + $\frac{1}{2}$)² + $\frac{15}{4}$.
∵b＜0，(b + $\frac{1}{2}$)²≥0，
∴AM≥$\frac{\sqrt{15}}{2}$.
在△AMN中，AN + MN≥AM，
∴当A、N、M三点共线，且AM = $\frac{\sqrt{15}}{2}$时，AN最小.
∵点N是以点M为圆心，1为半径的圆上的动点，
∴MN = 1，
∴AN = $\frac{\sqrt{15}}{2}$ - 1.

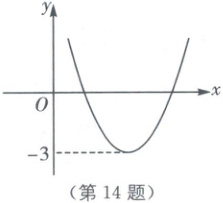
14. 如图,已知函数$ y = ax^2 + bx + c $的图像如图所示,则关于$ x $的方程$ ax^2 + bx + c + 2 = 0 $的根的情况是有两个同号不等实数根.

答案： 14.有两个同号不等实数根　[解析]由图可得y = ax² + bx + c的图像与x轴有两个交点，顶点的纵坐标是 - 3.
∵方程ax² + bx + c + 2 = 0，
∴ax² + bx + c = - 2，即y = - 2，由图像可知，有两个同号不等实数根.

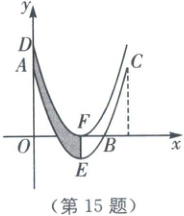
15. 如图,已知抛物线$ y = ax^2 + bx + 3 $经过点$ B(3, 0) $、$ C(4, 3) $,与$ y $轴交于点$ A $,把抛物线向上平移,使得顶点$ E $落在$ x $轴上点$ F $处,点$ A $平移至点$ D $处,则两条抛物线、对称轴$ EF $和$ y $轴围成的图形(图中阴影部分)的面积$ S = $2.

答案：
15.2　[解析]
∵抛物线y = ax² + bx + 3经过点B(3,0)、C(4,3)，
∴$\begin{cases}9a + 3b + 3 = 0 \\16a + 4b + 3 = 3 \end{cases}$，解得$\begin{cases}a = 1 \\b = - 4 \end{cases}$，
∴抛物线的函数表达式为y = x² - 4x + 3，
∴y = x² - 4x + 3 = (x - 2)² - 1，
∴抛物线的顶点坐标为(2,-1)，
∴EF = 1.
如图，由平移可知阴影部分的面积等于平行四边形AEFD的面积，平行四边形AEFD的面积 = 1×2 = 2，
∴S = 2.

16. (2023·滨州中考)某广场要建一个圆形喷水池,计划在池中心位置竖直安装一根顶部带有喷水头的水管,使喷出的抛物线形水柱在与池中心的水平距离为1 m处达到最高,高度为3 m,水柱落地处离池中心的水平距离也为3 m,那么水管的设计高度应为$\frac{9}{4}$m.

答案： 16.$\frac{9}{4}$m[解析]由题意可知，点(1,3)是抛物线的顶点，
∴设这段抛物线的表达式为y = a(x - 1)² + 3.
∵该抛物线过点(3,0)，
∴0 = a(3 - 1)² + 3，
解得a = -$\frac{3}{4}$，
∴y = -$\frac{3}{4}$(x - 1)² + 3.
∵当x = 0时，y = -$\frac{3}{4}$×(0 - 1)² + 3 = -$\frac{3}{4}$ + 3 = $\frac{9}{4}$，
∴水管的设计高度应为$\frac{9}{4}$m.

17. 已知函数$ y = kx^2 + (2k + 1)x + 1 $($ k $为实数),对于任意正实数$ k $,当$ x ＞ m $时,$ y $随着$ x $的增大而增大,则$ m $的取值范围是m≥ - 1.

答案： 17.m≥ - 1　[解析]
∵y = kx² + (2k + 1)x + 1(k为实数)，
∵k＞0，
∴该抛物线开口向上，对称轴为直线x = -$\frac{2k + 1}{2k}$ = - 1 - $\frac{1}{2k}$＜ - 1.
∵对于任意正实数k，当x＞m时，y随着x的增大而增大，
∴m≥ - 1.

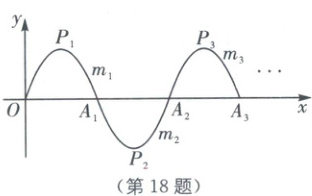
18. 中考新考法 规律探究 如图,一段抛物线$ y = -x(x - 1)(0 \leq x \leq 1) $记为$ m_1 $,它与$ x $轴交点为$ O $、$ A_1 $,顶点为$ P_1 $;将$ m_1 $绕点$ A_1 $旋转$ 180° $得$ m_2 $,交$ x $轴于点$ A_2 $,顶点为$ P_2 $;将$ m_2 $绕点$ A_2 $旋转$ 180° $得$ m_3 $交$ x $轴于点$ A_3 $,顶点为$ P_3 $,…,如此进行下去,直至得$ m_{10} $,顶点为$ P_{10} $,则$ P_{10} $的坐标为($\frac{19}{2}$,-$\frac{1}{4}$).

答案： 18.($\frac{19}{2}$,-$\frac{1}{4}$)　[解析]y = -x(x - 1) = -(x - $\frac{1}{2}$)² + $\frac{1}{4}$(0≤x≤1)，
∴P₁的坐标为($\frac{1}{2}$,$\frac{1}{4}$).
由题意，得OA₁ = A₁A₂ = 1，P₂P₄ = P₁P₃ = 2，
∴P₂的横坐标是$\frac{1 + 2}{2}$ = $\frac{3}{2}$，纵坐标是 -$\frac{1}{4}$，即P₂的坐标为($\frac{3}{2}$,-$\frac{1}{4}$)，
∴P₁₀的横坐标是$\frac{9 + 10}{2}$ = $\frac{19}{2}$，纵坐标是 -$\frac{1}{4}$，即P₁₀的坐标为($\frac{19}{2}$,-$\frac{1}{4}$).