《2025年实验班提优大考卷九年级数学上册苏科版》

8. (2023·通辽中考)如图,抛物线$y=ax^{2}+bx+c(a≠0)$与$x$轴交于点$(x_{1},0)、(2,0)$,其中$0＜x_{1}＜1$.下列四个结论:①$abc＜0$;②$a+b+c＞0$;③$2b+3c＜0$;④不等式$ax^{2}+bx+c＜-\frac{c}{2}x+c$的解集为$0＜x＜2$.其中正确结论的个数是(C).

A.1
B.2
C.3
D.4

答案：
8.C [解析]$\because$抛物线开口向上，对称轴在y轴右边，与y轴交于正半轴，$\therefore a ＞ 0$，$b ＜ 0$，$c ＞ 0$，$\therefore abc ＜ 0$，$\therefore$①正确；
$\because$当$x = 1$时，$y ＜ 0$，$\therefore a + b + c ＜ 0$，$\therefore$②错误；
$\because$抛物线过点$(2,0)$，$\therefore 4a + 2b + c = 0$，
$\therefore a = -\frac{1}{2}b - \frac{1}{4}c$.$\because a + b + c ＜ 0$，
$\therefore -\frac{1}{2}b - \frac{1}{4}c + b + c ＜ 0$，$\therefore \frac{1}{2}b + \frac{3}{4}c ＜ 0$，$\therefore$③正确；
设$y_1 = ax^2 + bx + c$，$y_2 = -\frac{c}{2}x + c$，由图知，当$y_1 ＜ y_2$时，$0 ＜ x ＜ 2$，故④正确.

综上所述，正确结论的个数为3.故选C.

9. 实验班原创 中学生骑电动车上学在交通安全上存在一定的隐患,为了了解某中学3 000名学生的家长对“中学生骑电动车上学”的态度,交通运输部门从中随机抽取了1 000名家长进行问卷调查.在这个调查中,样本容量是1000.

答案： 9.1000 [解析]根据样本容量是样本中包含的个体的数目，可知样本容量是1000.
归纳总结 本题主要考查了样本容量，关键是掌握样本容量只是数，没有单位.

10. (2023·锦州中考)一个不透明的盒子中装有若干个红球和5个黑球,这些球除颜色外均相同.经多次摸球试验后发现,摸到黑球的频率稳定在0.25左右,则盒子中红球的个数约为15.

答案： 10.15 [解析]由题意，知盒子中球的总个数为$5 ÷ 0.25 = 20$（个），所以盒子中红球的个数为$20 - 5 = 15$（个）.

11. 在一组数据1、3、5、7、$a$中,$a$为中位数,且$a$为整数,则这组数据的平均数为3.8或4或4.2.

答案： 11.3.8或4或4.2 [解析]$\because$整数a是这组数据的中位数，$\therefore a = 3$、$4$、$5$，$\therefore$这组数据的平均数$= \frac{1}{5} × (1 + 3 + 5 + 7 + 3) = 3.8$或$\frac{1}{5} × (1 + 3 + 5 + 7 + 4) = 4$或$\frac{1}{5} × (1 + 3 + 5 + 7 + 5) = 4.2$

12. (2024·宜宾中考)如图,正五边形ABCDE的边长为4,则这个正五边形的对角线AC的长是2√5+2.

答案：
12.$2\sqrt{5} + 2$ [解析]连接BE交AC于O，

$\because$五边形ABCDE是正五边形，
$\therefore \angle CBA = \angle BAE = (5 - 2) × 180^{\circ} ÷ 5 = 108^{\circ}$，$BC = AB = AE$，$\therefore \angle BCA = \angle BAC = \angle ABE = \angle AEB = (180^{\circ} - 108^{\circ}) ÷ 2 = 36^{\circ}$，
$\therefore \angle CBO = \angle ABC - \angle ABE = 108^{\circ} - 36^{\circ}$，
$\therefore \angle BOC = 180^{\circ} - \angle CBO - \angle BCA = 180^{\circ} - 72^{\circ} - 36^{\circ} = 72^{\circ}$，$\therefore \angle CBO = \angle BOC = 72^{\circ}$，$\therefore CO = BC = 4$.
$\because \angle BAO = \angle CAB$，$\angle ABO = 36^{\circ} = \angle BCA$，
$\therefore \triangle ABO \backsim \triangle ACB$，$\therefore \frac{AB}{AC} = \frac{AO}{AB}$，即$\frac{4}{AC} = \frac{AC - 4}{4}$
解得$AC = 2\sqrt{5} + 2$或$AC = 2 - 2\sqrt{5}$（负数，舍去），
显然$AC = 2\sqrt{5} + 2 ＞ OC = 4$，故$AC = 2\sqrt{5} + 2$.

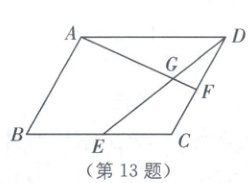
13. 教材P74习题T3·拓展 如图,在平行四边形ABCD中,E、F分别为BC、CD的中点,AF与DE相交于点G,则DG:EG=2:3.

答案：
13.2:3 [解析]如图，延长AF、BC交于点H，
$\because$四边形ABCD是平行四边形，E、F分别为BC、CD的中点，$\therefore CB // AD$，$BE = CE$，$CF = DF$，$\therefore CB = AD = 2CE$.
$\because HC // AD$，$\therefore \triangle HCF \backsim \triangle ADF$，$\therefore \frac{HC}{AD} = \frac{CF}{DF} = 1$，
$\therefore HC = AD = CB = 2CE$，
$\therefore HE = HC + CE = 2CE + CE = 3CE$.
$\because AD // HE$，$\therefore \triangle ADG \backsim \triangle HEG$，$\therefore \frac{DG}{EG} = \frac{AD}{HE} = \frac{2CE}{3CE} = \frac{2}{3}$，
$\therefore DG:EG = 2:3$.

14. 分类讨论思想(2024·牡丹江中考)矩形ABCD的面积是90,对角线AC、BD交于点O,点E是BC边的三等分点,连接DE,点P是DE的中点,OP=3,连接CP,则PC+PE的值为13或√109.

答案：
14.13或$\sqrt{109}$ [解析]当$CE ＞ BE$时，如图
(1)，
$\because$点O为矩形ABCD的对角线的交点，
$\therefore$点O是BD的中点，$\angle BCD = 90^{\circ}$.
$\because$点P是DE的中点，$OP = 3$，
$\therefore BE = 2OP = 6$，$CP = PE = PD$.
直角三角形斜边上的中线等于斜边的一半
$\because$点E是BC边的三等分点，且$CE ＞ BE$，
$\therefore CE = 2BE = 12$，$BC = 3BE = 18$.
$\because$矩形ABCD的面积是90，$\therefore BC · CD = 90$，$\therefore CD = 5$，
$\therefore DE = \sqrt{5^2 + 12^2} = 13$，
$\therefore PC + PE = DE = 13$；
当$CE ＜ BE$时，如图
(2)，
$\because$点O为矩形ABCD的对角线的交点.
$\therefore$点O是BD的中点.
$\because$点P是DE的中点，
$\therefore BE = 2OP = 6$，$CP = PE = PD$.

$\because$点E是BC边的三等分点，且$CE ＜ BE$，
$\therefore CE = \frac{1}{2}BE = 3$，$BC = 3 + 6 = 9$.
$\because$矩形ABCD的面积是90，$\therefore BC · CD = 90$，$\therefore CD = 10$，
$\therefore DE = \sqrt{3^2 + 10^2} = \sqrt{109}$，$\therefore PC + PE = DE = \sqrt{109}$.
解后反思 本题考查了矩形的性质、三角形中位线定理、勾股定理，解答本题的关键是熟练运用分类讨论思想解决问题.

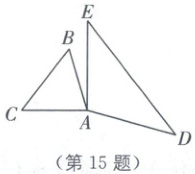
15. 手拉手模型(2025·南京江北新区旭东中学模拟)如图,在△ABC与△ADE中,$∠BAC+∠DAE=180^{\circ}$,AB=AC=5,BC=6,AD=AE=7,则DE的长为56/5.

答案：
15.$\frac{56}{5}$ [解析]如图，过点A作$AM \perp BC$于点M，$AN \perp DE$于点N.
$\because AB = AC = 5$，$BC = 6$，
$AM \perp BC$，
$\therefore BM = CM = 3$，
$\therefore \angle CAM = \angle BAM$，
$\therefore AM = \sqrt{AB^2 - BM^2} = \sqrt{5^2 - 3^2} = 4$.

$\because AE = AD$，$AN \perp DE$，
$\therefore NE = ND$，$\angle EAN = \angle DAN$.
$\because \angle CAB + \angle DAE = 180^{\circ}$，$\therefore \angle BAM + \angle EAN = 90^{\circ}$.
$\because \angle EAN + \angle E = 90^{\circ}$，$\therefore \angle BAM = \angle E$.
$\because \angle AMB = \angle ANE = 90^{\circ}$，$\therefore \triangle AMB \backsim \triangle ENA$，
$\therefore \frac{AM}{EN} = \frac{AB}{AE}$，$\therefore \frac{4}{EN} = \frac{5}{7}$，$\therefore EN = \frac{28}{5}$，
$\therefore DE = 2EN = \frac{56}{5}$.

16. (2025·泰州兴化期末)在平面直角坐标系中,已知二次函数$y=mx^{2}-4m^{2}x-1(m≠0)$,A$(3m-1,y_{1})$、B$(2m,y_{2})$、C$(2m+3,y_{3})$为抛物线上的点,若$y_{1}＞y_{3}＞y_{2}$,则$m$的取值范围是m＞4.

答案： 16.$m ＞ 4$ [解析]因为二次函数解析式为$y = mx^2 - 4m^2x - 1(m \neq 0)$，
所以抛物线的对称轴为直线$x = \frac{-(-4m^2)}{2m} = 2m$.
因为$A(3m - 1,y_1)$、$B(2m,y_2)$、$C(2m + 3,y_3)$，
所以点B为抛物线的顶点.
又因为$y_1 ＞ y_3 ＞ y_2$，所以抛物线的开口向上，
则$m ＞ 0$，且$|3m - 1 - 2m| ＞ |2m + 3 - 2m|$，
解得$m ＞ 4$，所以m的取值范围是$m ＞ 4$.

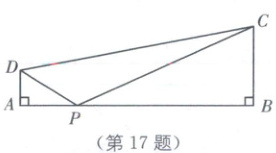
17. 分类讨论思想 如图,在四边形ABCD中,$∠A=∠B=90^{\circ}$,AB=6,AD=1,BC=2,P为AB边上的动点,当△PAD与△PBC相似时,$PA=$2或3+√7或3-√7.

答案： 17.2或$3 + \sqrt{7}$或$3 - \sqrt{7}$ [解析]$\because \angle A = \angle B = 90^{\circ}$，$AB = 6$，$AD = 1$，$BC = 2$，$\therefore$设AP的长为x，则BP长为$6 - x$.
若AB边上存在P点，使$\triangle PAD$与$\triangle PBC$相似，可以分为两种情况：
①当$\angle APD = \angle BPC$时，$\triangle APD \backsim \triangle BPC$，
则$AP:BP = AD:BC$，即$x:(6 - x) = 1:2$，
解得$x = 2$.
②当$\angle APD = \angle BCP$时，$\triangle APD \backsim \triangle BPC$，
则$AP:BC = AD:BP$，即$x:2 = 1:(6 - x)$，
解得$x = 3 \pm \sqrt{7}$.
综上所述，$PA = 2$或$3 + \sqrt{7}$或$3 - \sqrt{7}$.

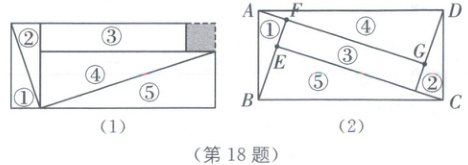
18. (2025·淮安期末)图(1)中周长为20的矩形纸片剪掉一块边长为1的正方形后,将剩下的部分沿线剪开,拼成不重叠、无缝隙的矩形ABCD(如图(2)),则图(2)中$\\tan∠BCE=$1/3.

答案： 18.$\frac{1}{3}$ [解析]由题意，得$\angle AFB = \angle BEC = 90^{\circ}$，$AF = EF = 1$.
$\because$图
(1)的矩形纸片周长为20，
$\therefore$图
(1)的大矩形的长与宽的和为10，
$\therefore$设$FG = a$，则$BF = 10 - a - 1 - 1 = 8 - a$.
$\because$四边形ABCD是矩形，
$\therefore \angle ABC = 90^{\circ}$，$\therefore \angle ABE + \angle EBC = 90^{\circ}$.
$\because \angle EBC + \angle BCE = 90^{\circ}$，
$\therefore \angle ABF = \angle BCE$，$\therefore \triangle AFB \backsim \triangle BEC$，
$\therefore \frac{AF}{BE} = \frac{BF}{CE}$，$\therefore \frac{1}{8 - a} = \frac{a + 1}{1}$，
解得$a = 5$或$a = 11$（舍去），
$\therefore BE = BF - 1 = 8 - 5 - 1 = 2$，$CE = 5 + 1 = 6$，
在$Rt \triangle BCE$中，$\tan \angle BCE = \frac{BE}{CE} = \frac{2}{6} = \frac{1}{3}$.