《2025年实验班提优大考卷九年级数学上册苏科版》

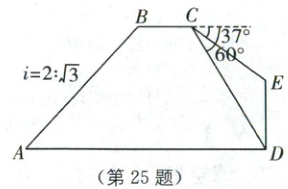
25. (8分)(2023·泸州中考)如图,某数学兴趣小组为了测量古树DE的高度,采用了如下的方法:先从古树底端D在同一水平线上的点A出发,沿斜面坡度为$i=2:\\sqrt{3}$的斜坡AB前进$20\\sqrt{7}$m到达点B,再沿水平方向继续前进一段距离后到达点C.在点C处测得古树DE的顶端E的俯角为$37^{\\circ}$,底部D的俯角为$60^{\\circ}$,求古树DE的高度.(参考数据:$\\sin37^{\\circ}≈\frac{3}{5}$,$\\cos37^{\\circ}≈\frac{4}{5}$,$\\tan37^{\\circ}≈\frac{3}{4}$,计算结果用根号表示,不取近似值)

答案： 25.过点B作$BF \perp AD$于点F，
在$Rt \triangle ABF$中，$\because i = 2:\sqrt{3}$，
$\therefore$可设$BF = 2k$，$AF = \sqrt{3}k$.
$\because AB = 20\sqrt{7}$m，$BF^2 + AF^2 = AB^2$，
$\therefore (2k)^2 + (\sqrt{3}k)^2 = (20\sqrt{7})^2$，
解得$k = 20$（负值已舍），$\therefore BF = 2k = 40$m.
延长BC、DE交于点H，
$\because BC$是水平线，$DE$是铅直线，$\therefore \triangle CDH$和$\triangle CEH$都是直角三角形.
$\because AD$、$BC$都是水平线，$BF \perp AD$，$DH \perp BC$，
$\therefore$四边形$BFDH$是矩形，$\therefore DH = BF = 40$m.
在$Rt \triangle CDH$中，$\because \tan \angle DCH = \frac{DH}{CH}$，
$\therefore CH = \frac{DH}{\tan \angle DCH} = \frac{40}{\tan 60^{\circ}} = \frac{40\sqrt{3}}{3}$(m).
在$Rt \triangle CEH$中，$\because \tan \angle ECH = \frac{EH}{CH}$，
$\therefore EH = CH · \tan \angle ECH = \frac{40\sqrt{3}}{3} · \tan 37^{\circ} \approx \frac{40\sqrt{3}}{3} × \frac{3}{4} = 10\sqrt{3}$(m)，$\therefore DE = DH - EH = (40 - 10\sqrt{3})$m.
故古树DE的高度为$(40 - 10\sqrt{3})$m.

26. (8分)跨学科 古诗词理解(2024·乐山中考)我国明朝数学家程大位写过一本数学著作《直指算法统宗》,其中有一道与荡秋千有关的数学问题是使用《西江月》词牌写的:
平地秋千未起,踏板一尺离地.
送行二步与人齐,五尺人高曾记.
仕女佳人争蹴,终朝笑语欢嬉.
良工高士素好奇,算出索长有几?
词写得很优美,翻译成现代汉语的大意是:有一架秋千,当它静止时,踏板离地1尺,将它往前推进10尺(5尺为一步),秋千的踏板就和某人一样高,这个人的身高为5尺.(假设秋千的绳索拉的很直)
(1)如图(1),请你根据词意计算秋千绳索OA的长度.
(2)如图(2),将秋千从与竖直方向夹角为α的位置$OA'$释放,秋千摆动到另一侧与竖直方向夹角为β的地方$OA''$,两次位置的高度差$PQ=h$.根据上述条件能否求出秋千绳索OA的长度？如果能,请用含α、β和h的式子表示;如果不能,请说明理由.

答案：
26.
(1)如图，过点$A^{\prime}$作$A^{\prime}B \perp OA$于点B.

设秋千绳索的长度为x尺.
由题可知，$OA = OA^{\prime} = x$尺，$AB = 5 - 1 = 4$（尺），
$\therefore A^{\prime}B = 10$尺，$\therefore OB = OA - AB = (x - 4)$尺.
在$Rt \triangle OA^{\prime}B$中，由勾股定理，得$A^{\prime}B^2 + OB^2 = OA^{\prime 2}$，
$\therefore 10^2 + (x - 4)^2 = x^2$，解得$x = 14.5$.
故秋千绳索的长度为14.5尺.
(2)能.理由如下：由题可知，
$\angle OP A^{\prime} = \angle OQ A^{\prime \prime} = 90^{\circ}$，$OA^{\prime} = OA^{\prime \prime} = OA$.
在$Rt \triangle OA^{\prime}P$中，$\cos \alpha = \frac{OP}{OA^{\prime}}$，
$\therefore OP = OA^{\prime} · \cos \alpha = OA · \cos \alpha$.
同理，$OQ = OA^{\prime \prime} · \cos \beta = OA · \cos \beta$.
$\because OQ - OP = h$，$\therefore OA · \cos \beta - OA · \cos \alpha = h$，
$\therefore OA · (\cos \beta - \cos \alpha) = h$，$\therefore OA = \frac{h}{\cos \beta - \cos \alpha}$.