第164页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
10. 如图(1),现有长2,宽1的$A$、$B$两种卡片各若干张,卡片上都有一条对角线花纹,请用这些卡片正好拼成一个$10 × 10$的大正方形,要求每张卡片与卡片的对角线都不相连(例如图(2)中所示的两种拼法就都不符合要求),则$A$、$B$两种卡片各需要的张数可能是(
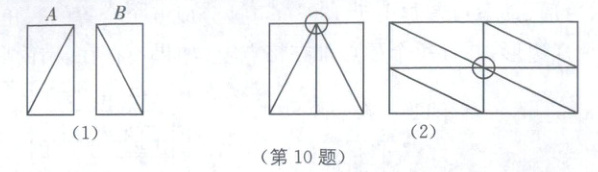
A.30、20
B.28、22
C.26、24
D.25、25
A
).
A.30、20
B.28、22
C.26、24
D.25、25
答案:
10.A [解析]
∵用长2,宽1的A、B两种卡片各若干张拼成一个$10×10$的大正方形,
∴每张卡片的面积为$2×1=2$,大正方形的面积为$10×10=100$,
∴大正方形的边长为10.
设A卡片的数量为x,B卡片的数量为y,
∴$2x+2y=100$,
∴$x+y=50$.
为避免对角线相连,将A卡片顺时针旋转使对角线为左上到右下(横向),B卡片为左上到右下(纵向),如图所示,

其中A卡片(横向)共有30张,B卡片(纵向)共有20张.故选A.
10.A [解析]
∵用长2,宽1的A、B两种卡片各若干张拼成一个$10×10$的大正方形,
∴每张卡片的面积为$2×1=2$,大正方形的面积为$10×10=100$,
∴大正方形的边长为10.
设A卡片的数量为x,B卡片的数量为y,
∴$2x+2y=100$,
∴$x+y=50$.
为避免对角线相连,将A卡片顺时针旋转使对角线为左上到右下(横向),B卡片为左上到右下(纵向),如图所示,

其中A卡片(横向)共有30张,B卡片(纵向)共有20张.故选A.
11. 计算:$5\sqrt {3} -3\sqrt {3} =$
$2\sqrt{3}$
.
答案:
11.$2\sqrt{3}$ [解析]本题考查二次根式的运算.根据二次根式的减法法则,得$5\sqrt{3}-3\sqrt{3}=2\sqrt{3}$.
12. 3月15日,我国动画电影《哪吒2》已跻身全球影史票房排行榜的第五位,《哪吒2》向世界观众展现了中国动画的风采和中华文化的魅力.为实现高水平的视觉效果,全片共有1 900多个特效镜头,数据1 900用科学记数法表示为
$1.9×10^{3}$
.
答案:
12.$1.9×10^{3}$ [解析]本题考查科学记数法的表示方法.$1900=1.9×10^{3}$.
13. 已知点$P(m +1,2m)$在正比例函数$y =x$的图像上,则$m =$
1
.
答案:
13.1 [解析]本题考查正比例函数图像上的点.根据点P在正比例函数$y=x$的图像上,可得点P的坐标满足$y=x$,即$2m=m+1$,解得$m=1$.
14. 央视春晚无锡分会场主舞台所在的清名桥历史文化街区,今年大年初一接待游客20万人次,大年初三接待游客22万人次,若设平均每天游客人数增长的百分率为$x$,根据题意可得方程为
$20(1+x)^{2}=22$
.
答案:
14.$20(1+x)^{2}=22$ [解析]本题考查一元二次方程的应用,关键是找准等量关系.因为大年初一接待游客20万人次,平均每天游客人数增长的百分率为x,所以大年初二接待游客$20(1+x)$人次,大年初三接待游客$20(1+x)^{2}$人次,所以$20(1+x)^{2}=22$.
15. 当蓄电池的电压为定值时,电流$I$(单位:A)与电阻$R$(单位:$\Omega$)是反比例函数关系,它的图像如图所示.当电阻$R$的取值范围是
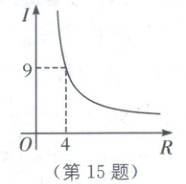
$R\geqslant3\Omega$
时,电流$I \leq 12$ A.
答案:
15.$R\geqslant3\Omega$ [解析]本题考查反比例函数的图像特征.根据图像可得反比例函数的表达式为$I=\frac{36}{R}$,当$I=12A$时,$R=3\Omega$.又反比例函数的图像在第一象限,且I随R的增大而减小,所以当$R\geqslant3\Omega$时,$I\leqslant12A$.
16. 如图,在$□ ABCD$中,点$E$在$AD$上,且$EC$平分$\angle BED$,若$\angle EBC = 30^{\circ}$,$BE =8$,则$□ ABCD$的面积为

32
.
答案:
16.32 [解析]本题考查平行四边形的性质、等腰三角形的判定以及含$30^{\circ}$角的直角三角形的性质.
∵四边形ABCD是平行四边形,$AD// BC$,
∴$\angle DEC=\angle ECB$.
∵EC平分$\angle BED$,
∴$\angle DEC=\angle BEC$,
∴$\angle BEC=\angle ECB$,
∴$BE=BC$.
∵$BE=8$,
∴$BC=8$.过点E作$EF\perp BC$.
∵$\angle EBC=30^{\circ}$,
∴$EF=\frac{1}{2}BE=4$,
∴$S_{□ ABCD}=BC· EF=8×4=32$.
∵四边形ABCD是平行四边形,$AD// BC$,
∴$\angle DEC=\angle ECB$.
∵EC平分$\angle BED$,
∴$\angle DEC=\angle BEC$,
∴$\angle BEC=\angle ECB$,
∴$BE=BC$.
∵$BE=8$,
∴$BC=8$.过点E作$EF\perp BC$.
∵$\angle EBC=30^{\circ}$,
∴$EF=\frac{1}{2}BE=4$,
∴$S_{□ ABCD}=BC· EF=8×4=32$.
17. 已知点$(-1,m)$和点$(-5,n)$都在二次函数$y = ax^{2} + bx(a < 0)$的图像上,且$mn < 0$.若点$(2,y_{1})$、$(-2,y_{2})$、$(-6,y_{3})$也都在这个函数的图像上,则$y_{1}$、$y_{2}$、$y_{3}$的大小关系为
$y_{3}<y_{1}<y_{2}$
.(用“<”连接)
答案:
17.$y_{3}<y_{1}<y_{2}$ [解析]
∵点$(-1,m)$和点$(-5,n)$都在二次函数$y=ax^{2}+bx(a<0)$的图像上,
∴$m=a-b$,$n=25a-5b$.
∵$mn<0$,
∴$(a-b)(25a-5b)<0$,解得$5a<b<a<0$.
当$x=2$时,$y_{1}=4a+2b$,当$x=-2$时,$y_{2}=4a-2b$,当$x=-6$时,$y_{3}=36a-6b$,
故$y_{1}-y_{2}=4a+2b-(4a-2b)=4b<0$,即$y_{1}<y_{2}$;
$y_{3}-y_{2}=36a-6b-(4a-2b)=32a-4b=8(4a-b)$.
∵$5a<b<a<0$,
∴$3a<4a-b<-a<0$,$y_{3}<y_{1}$.
故$y_{3}<y_{1}<y_{2}$.
∵点$(-1,m)$和点$(-5,n)$都在二次函数$y=ax^{2}+bx(a<0)$的图像上,
∴$m=a-b$,$n=25a-5b$.
∵$mn<0$,
∴$(a-b)(25a-5b)<0$,解得$5a<b<a<0$.
当$x=2$时,$y_{1}=4a+2b$,当$x=-2$时,$y_{2}=4a-2b$,当$x=-6$时,$y_{3}=36a-6b$,
故$y_{1}-y_{2}=4a+2b-(4a-2b)=4b<0$,即$y_{1}<y_{2}$;
$y_{3}-y_{2}=36a-6b-(4a-2b)=32a-4b=8(4a-b)$.
∵$5a<b<a<0$,
∴$3a<4a-b<-a<0$,$y_{3}<y_{1}$.
故$y_{3}<y_{1}<y_{2}$.
18. 在平面直角坐标系中,已知$A(0,0)$,$B(6,0)$,$C(m,\sqrt {5})$,$D(m +6,\sqrt {5})$.分别连接$AB$、$BC$、$AC$,把$\triangle ABC$沿$BC$翻折得到$\triangle A'BC$.当$A'$与$D$重合时,$BD =$
6
;当以$A'$、$C$、$B$、$D$为顶点的四边形是矩形时,$m =$1或5或6
.
答案:
18.1或5或6 [解析]如图
(1)
(2)所示,$A(0,0)$,$B(6,0)$,$C(m,\sqrt{5})$,$D(m+6,\sqrt{5})$,
∴$AB=6$,$CD=6$,$AB// CD$,且点C、D在直线$y=\sqrt{5}$上,
∴$AB=CD$,
∴四边形ABDC是平行四边形.
将$\triangle ABC$沿BC翻折得到$\triangle A'BC$,且$A'$与D重合,
∴$AB=BD=AC=CD=6$.
如图
(3)
(4),
∵四边形$A'CBD$是矩形,
∴$\angle A'CB=90^{\circ}$.
由折叠得$\angle ACB=\angle A'CB=90^{\circ}$,
∴$AC^{2}+BC^{2}=AB^{2}$,
∴$m^{2}+5+(m-6)^{2}+5=36$,
解得$m=1$或$m=5$.

如图
(5),
∵四边形$A'BCD$是矩形,
∴$\angle A'BC=\angle ABC=90^{\circ}$,$A'B=AB=CD=6$,
∴$m=6$.
综上,当以$A'$、B、C、D为顶点的四边形是矩形时,$m=1$或5或6.
18.1或5或6 [解析]如图
(1)
(2)所示,$A(0,0)$,$B(6,0)$,$C(m,\sqrt{5})$,$D(m+6,\sqrt{5})$,
∴$AB=6$,$CD=6$,$AB// CD$,且点C、D在直线$y=\sqrt{5}$上,
∴$AB=CD$,
∴四边形ABDC是平行四边形.
将$\triangle ABC$沿BC翻折得到$\triangle A'BC$,且$A'$与D重合,
∴$AB=BD=AC=CD=6$.
如图
(3)
(4),
∵四边形$A'CBD$是矩形,
∴$\angle A'CB=90^{\circ}$.
由折叠得$\angle ACB=\angle A'CB=90^{\circ}$,
∴$AC^{2}+BC^{2}=AB^{2}$,
∴$m^{2}+5+(m-6)^{2}+5=36$,
解得$m=1$或$m=5$.

如图
(5),
∵四边形$A'BCD$是矩形,
∴$\angle A'BC=\angle ABC=90^{\circ}$,$A'B=AB=CD=6$,
∴$m=6$.
综上,当以$A'$、B、C、D为顶点的四边形是矩形时,$m=1$或5或6.
19. (8分)解不等式组$\begin{cases} \begin{array}{l} {5x -2 > 3(x -2), } \\ { \dfrac {1}{2}x -3 \leq 1 - \dfrac {3}{2}x, } \end{array} \end{cases} $并写出该不等式组整数解.
答案:
19.[解析]本题考查了解一元一次不等式组及整数解.先分别解出两个不等式的解集,再根据“同大取大,同小取小,大小小大中间找,大大小小找不到”得出不等式组的解集,最后写出整数解即可.
$\begin{cases}5x-2>3(x-2),&①\frac{1}{2}x-3\leqslant1-\frac{3}{2}x.&②\end{cases}$
由①得$x>-2$,由②得$x\leqslant2$,
所以不等式组的解为$-2<x\leqslant2$,
所以该不等式组的整数解为-1、0、1、2.
$\begin{cases}5x-2>3(x-2),&①\frac{1}{2}x-3\leqslant1-\frac{3}{2}x.&②\end{cases}$
由①得$x>-2$,由②得$x\leqslant2$,
所以不等式组的解为$-2<x\leqslant2$,
所以该不等式组的整数解为-1、0、1、2.
查看更多完整答案,请扫码查看


