《2025年提分教练九年级数学上册人教版》

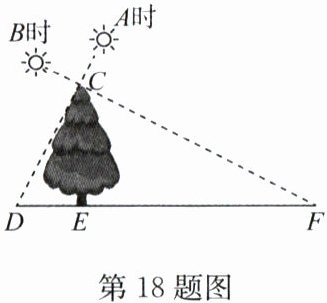
18. (10 分)如图,小明在 $ A $ 时测得某树的影长 $ DE $ 为 2 m,在 $ B $ 时又测得该树的影长 $ EF $ 为 8 m,若两次日照的光线互相垂直,求树的高度 $ CE $.

答案： 解:在Rt△CDF中，树高为CE，∠DCF=90°，
∴Rt△EDC∽Rt△ECF，
∴$\frac{EC}{EF}=\frac{ED}{EC}$，
∵DE=2m，EF=8m，
∴EC²=ED·EF，
∴EC²=2×8=16，
∴EC=4m，
∴树的高度CE是4m.

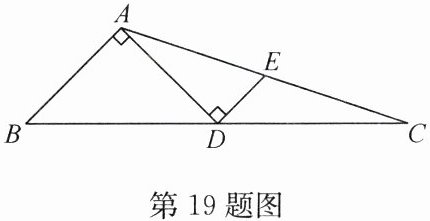
19. (11 分)如图,在 $ \triangle ABC $ 中,点 $ D $ 为 $ BC $ 边上的一点,且 $ AD = AB = 2 $,$ AD \perp AB $,过点 $ D $ 作 $ DE \perp AD $,$ DE $ 交 $ AC $ 于点 $ E $,若 $ DE = 1 $,求 $ \triangle ABC $ 的面积.

答案： 解:
∵AB⊥AD，DE⊥AD，
∴∠BAD=∠ADE=90°，
∴AB//DE，
∴△CDE∽△CBA，
∴$\frac{DC}{BC}=\frac{DE}{BA}=\frac{1}{2}$，
∴CD=BD.
由题得$BD=2\sqrt{2}$，
∴$DC=2\sqrt{2}$，
∴$BC=4\sqrt{2}$.
过点A作AF⊥BC于点F，则易得$AF=\sqrt{2}$，
∴$S_{\triangle ABC}=\frac{1}{2}BC\cdot AF=\frac{1}{2}×4\sqrt{2}×\sqrt{2}=4$.

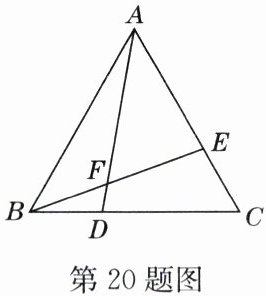
20. (11 分)如图所示,$ \triangle ABC $ 是等边三角形,点 $ D $,$ E $ 分别在 $ BC $,$ AC $ 上,且 $ CE = BD $,$ BE $,$ AD $ 相交于点 $ F $.
求证：(1)$ \triangle ABD \cong \triangle BCE $；
(2)$ \triangle AEF \sim \triangle BEA $.

答案： 证明:
(1)
∵△ABC是等边三角形，
∴AB=BC，∠ABD=∠C=60°.
在△ABD和△BCE中，
$\begin{cases}AB = BC\\∠ABD = ∠C\\BD = CE\end{cases}$，
∴△ABD≌△BCE(SAS).
(2)
∵△ABD≌△BCE，
∴∠BAD=∠CBE，
∴∠EAF=∠ABE.
又
∵∠AEF=∠BEA，
∴△AEF∽△BEA.

21. (13 分)水果店销售某种水果,该种水果的进价为 10 元/kg. 根据以往的销售经验可知：日销量 $ y $(单位：kg)随售价 $ x $(单位：元/kg)的变化规律符合某种函数关系. 该水果店以往的销售记录如下表：(售价不低于进价)

若 $ y $ 与 $ x $ 之间的函数关系是一次函数,二次函数,反比例函数中的某一种.
(1)判断 $ y $ 与 $ x $ 之间的函数关系,并写出其解析式.
(2)水果店销售该种水果的日利润能否达到 200 元？说明理由.

答案： 解:
(1)观察可知，售价x与日销量y的乘积为定值300，
故y与x之间为反比例函数关系，设函数解析式为$y=\frac{k}{x}$(k≠0)，当x=10时，y=30，
∴k=300，
∴函数解析式为$y=\frac{300}{x}$；
(2)能达到200元.
理由:依题意，得$(x - 10)\cdot\frac{300}{x}=200$，解得x=30，
经检验，得x=30是原方程的解，并且符合题意，
故当售价为30元/kg时，水果店销售该种水果的日利润为200元.