《2025年提分教练九年级数学上册人教版》

15. (10 分)如图,$ 10×8 $ 的网格中每个小正方形的边长均为 1,$ A、B、C $ 三点在小正方形的顶点上,请在图①、②中各画一个凸四边形,使其分别满足以下要求:
(1)请在图①中取一点 $ D $(点 $ D $ 必须在小正方形的顶点上),使以 $ A、B、C、D $ 为顶点的四边形是中心对称图形,但不是轴对称图形;
(2)请在图②中取一点 $ D $(点 $ D $ 必须在小正方形的顶点上),使以 $ A、B、C、D $ 为顶点的四边形是轴对称图形,但不是中心对称图形.

答案：
解:答案不唯一,如
(1)如图①所示,四边形ACBD即为所求.
(2)如图②所示,四边形ABCD即为所求.

16. (10 分)如图,已知点 $ A,B $ 的坐标分别为 $ (0,0) $,$ (4,0) $,将 $ \triangle ABC $ 绕点 $ A $ 按逆时针方向旋转 $ 90^{\circ} $ 得到 $ \triangle AB'C' $.
(1)画出 $ \triangle AB'C' $.
(2)写出点 $ C' $ 的坐标.
(3)求 $ BB' $ 的长.

答案：
解:
(1)
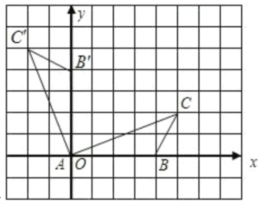
(2)根据旋转的性质,得点$C'$的坐标为(-2,5).
(3)$BB'=\sqrt{AB^{2}+AB'^{2}}=\sqrt{4^{2}+4^{2}}=4\sqrt{2}$.

17. (12 分)如图,点 $ E $ 是正方形 $ ABCD $ 的边 $ DC $ 上一点,把 $ \triangle ADE $ 按顺时针方向旋转到 $ \triangle ABF $ 的位置.
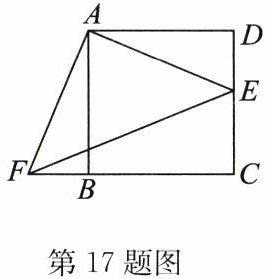
(1)旋转中心是点A,旋转角是90$ ^{\circ} $.
(2)若连接 $ EF $,则 $ \triangle AEF $ 是等腰直角三角形,并证明.
证明如下:
∵$\triangle ABF$是由$\triangle ADE$旋转所得,
$\therefore AF=AE$,$\angle FAB=\angle EAD$.
由正方形ABCD知$\angle BAE+\angle EAD=90^{\circ}$,
$\therefore \angle FAB+\angle BAE=90^{\circ}$.$\therefore \triangle AEF$是等腰直角三角形.
(3)若四边形 $ AECF $ 的面积为 25,$ DE = 2 $,求 $ AE $ 的长.
由题意,得$\triangle ADE\cong \triangle ABF$,
$\therefore S_{四边形AECF}=S_{正方形ABCD}=25$,$\therefore AD=5$.
又$\angle D=90^{\circ}$,$DE=2$,$\therefore AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{29}$.

答案：
(1)A 90
(2)等腰直角.证明如下:
∵$\triangle ABF$是由$\triangle ADE$旋转所得,
$\therefore AF=AE$,$\angle FAB=\angle EAD$.
由正方形ABCD知$\angle BAE+\angle EAD=90^{\circ}$,
$\therefore \angle FAB+\angle BAE=90^{\circ}$.$\therefore \triangle AEF$是等腰直角三角形.
(3)由题意,得$\triangle ADE\cong \triangle ABF$,
$\therefore S_{四边形AECF}=S_{正方形ABCD}=25$,$\therefore AD=5$.
又$\angle D=90^{\circ}$,$DE=2$,$\therefore AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{29}$.

18. (10 分)某公司为了节约开支,购买了质量相同的两种颜色的残缺地砖,准备用来装修地面,现已加工成如图①的等腰直角三角形,王聪同学设计了如图②的四种图案.

(1)你喜欢哪种图案？简述该图案的形成过程.
(2)请你利用所学过的知识再设计一幅与上述不同的图案.

答案：
解:
(1)我喜欢图案d.(答案不唯一)
图案d的形成过程:以同行或同列的两个小正方形组成的矩形为"基本图案",绕大正方形的中心旋转$180^{\circ}$得到.
(2)如图.(答案不唯一)