《2025年提分教练九年级数学上册人教版》

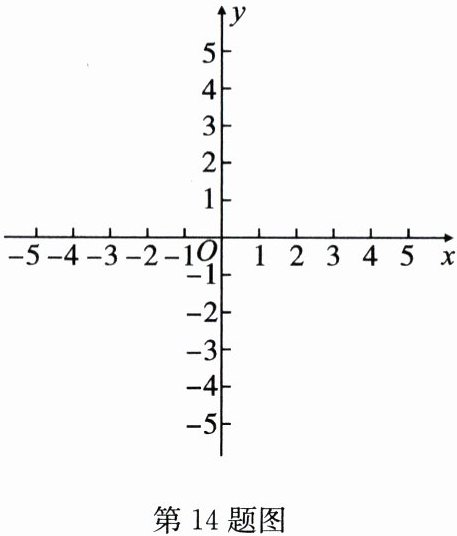
14. (9 分)在平面直角坐标系中,抛物线 $ y = ax^{2}+bx + 3 $ 经过点 $ A(3,0) $ 和点 $ B(4,3) $.
(1) 求这条抛物线所对应的二次函数的解析式；
(2) 直接写出该抛物线的开口方向和顶点坐标；
(3) 直接在所给的平面直角坐标系中画出这条抛物线.

答案：
解:
(1)
∵抛物线$y=ax^{2}+bx+3$经过点A(3,0)和点B(4,3),$\therefore \left\{\begin{array}{l} 9a+3b+3=0\\ 16a+4b+3=3\end{array}\right. $,解得$\left\{\begin{array}{l} a=1\\ b=-4\end{array}\right. $.
∴这条抛物线所对应的二次函数的解析式为$y=x^{2}-4x+3$.
(2)抛物线开口向上.顶点坐标为(2,−1).
(3)画出这条抛物线如图.

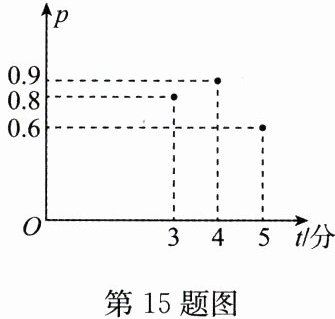
15. (9 分)在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”. 在特定条件下,“可食用率”$ p $ 与加工煎炸时间 $ t $(单位：分)近似满足的函数关系为 $ p = at^{2}+bt + c(a \neq 0,a,b,c $ 是常数),如图记录了三次试验的数据.
(1) 求 $ p $ 与 $ t $ 的解析式；
(2) 加工煎炸臭豆腐的最佳时间是多少？

答案： 解:
(1)将图象中的三个点(3,0.8)、(4,0.9)、(5,0.6)的坐标代入$p=at^{2}+bt+c$中,得$\left\{\begin{array}{l} 9a+3b+c=0.8\\ 16a+4b+c=0.9\\ 25a+5b+c=0.6\end{array}\right. $,解得$\left\{\begin{array}{l} a=-0.2\\ b=1.5\\ c=-1.9\end{array}\right. $.所以p与t的解析式为$p=-0.2t^{2}+1.5t-1.9$.
(2)由题意可知，加工煎炸臭豆腐的最佳时间为抛物线顶点的横坐标，$t=-\frac {b}{2a}=-\frac {1.5}{2×(-0.2)}=3.75$.故加工煎炸臭豆腐的最佳时间为3.75分钟.

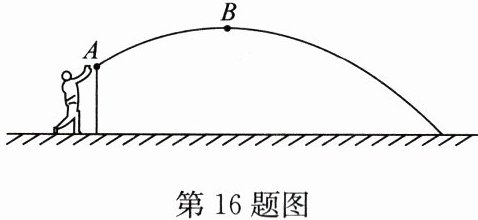
16. (10 分)为了在校运会投铅球比赛中取得更好的成绩,小丁积极训练. 在某次试投中铅球所经过的路线是如图所示的抛物线的一部分. 已知铅球出手处 $ A $ 距离地面的高度是 $ \frac{8}{5} $ 米,当铅球运行的水平距离为 $ 3 $ 米时,到达最大高度 $ \frac{5}{2} $ 米的 $ B $ 处. 小丁此次投掷的成绩是多少米？

答案：
解:建立平面直角坐标系如图所示.由题意，知点A的坐标为$(0,\frac {8}{5})$，顶点为$B(3,\frac {5}{2})$.设抛物线的解析式为$y=a(x - 3)^{2}+\frac {5}{2}$.
∵点$A(0,\frac {8}{5})$在抛物线上，$\therefore a(0 - 3)^{2}+\frac {5}{2}=\frac {8}{5}$，解得$a=-\frac {1}{10}$.
∴抛物线的解析式为$y=-\frac {1}{10}(x - 3)^{2}+\frac {5}{2}$.令$y=0$，则$-\frac {1}{10}(x - 3)^{2}+\frac {5}{2}=0$，解得$x=8$或$x=-2$(不合实际，舍去).即$OC=8$米.答:小丁此次投掷的成绩是8米.

17. (10 分)已知关于 $ x $ 的二次函数 $ y = (m - 2)x^{m^{2}+m - 4}+8x $.
(1) 求 $ m $ 的值；
(2) 设 $ P(5,p),Q(7,q) $ 都是该函数图象上的点,请比较 $ p $ 与 $ q $ 的大小.

答案： 解:
(1)由题可得$m^{2}+m - 4=2$且$m≠2$，解得$m_{1}=-3$，$m_{2}=2$(舍).故$m=-3$.
(2)由
(1)可得$y=-5x^{2}+8x$，则抛物线的对称轴为直线$x=\frac {4}{5}$，开口向下，
∴点P，Q都位于该抛物线对称轴的右侧，
∵在对称轴的右侧，函数值y随x的增大而减小，且$5＜7$，
∴$p＞q$.