《2025年提分教练九年级数学上册人教版》

18. (16 分)在一个不透明的盒子中装有大小和形状相同的 3 个红球和 2 个白球,把它们充分搅匀.
(1)“从中任意摸取 1 个球不是红球就是白球”是______事件,“从中任意摸取 1 个球是黑球”是______事件.
(2)从中任意摸取 1 个球恰好是红球的概率是______.
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则：从盒子中任取两个球,若两球同色,则选甲；若两球异色,则选乙. 你认为这个规则公平吗？请用列表法或画树状图法加以说明.

答案：
解:
(1)“从中任意摸取1个球不是红球就是白球”是必然事件，“从中任意摸取1个球是黑球”是不可能事件.
(2)从中任意摸取1个球恰好是红球的概率是$\frac{3}{5}$.
(3)这个规则不公平.记3个红球分别为红1，红2，红3,2个白球分别为白1，白2.画树状图如下:

　由树状图可得，一共有20种等可能的结果，其中两球同色的结果有8种，故选择甲的概率为$\frac{8}{20}=\frac{2}{5}$，则选择乙的概率为$\frac{3}{5}$.$\because \frac{2}{5}\neq \frac{3}{5}$，$\therefore$这个规则不公平.

19. (17 分)某艺校音乐专业自主招生考试中,所有考生均参加了“声乐”和“器乐”两个科目的考试,成绩都分为五个等级. 对某考场考生两科考试成绩进行了统计分析,绘制了如下统计表和统计图(不完整).


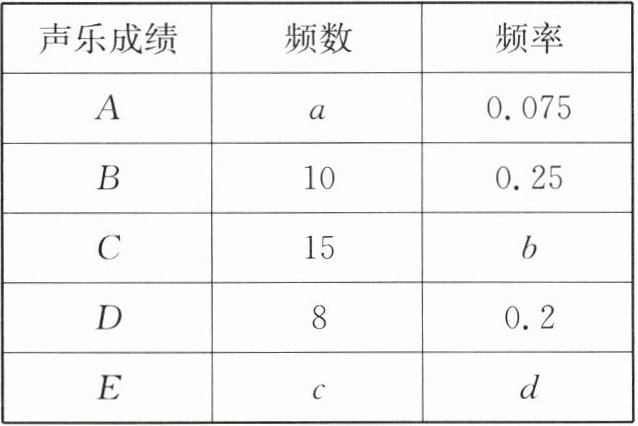
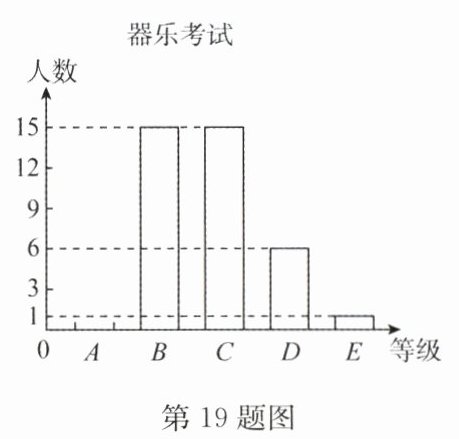
根据以上信息,解答下列问题：
(1)求表中 $ a $,$ b $,$ c $,$ d $ 的值,并补全条形统计图；
(2)若等级 $ A $,$ B $,$ C $,$ D $,$ E $ 分别对应 10 分,8 分,6 分,4 分,2 分,求该考场“声乐”科目考试成绩的平均分；
(3)已知本考场参加测试的考生中,恰有两人的这两科成绩均为 $ A $,在至少一科成绩为 $ A $ 的考生中,随机抽取两人进行面试,求这两人的两科成绩均为 $ A $ 的概率.

答案： 解:
(1)此考场的考生人数为$\frac{10}{0.25}=40$，则$a=40× 0.075=3$，$b=\frac{15}{40}=0.375$，$c=40-3-10-15-8=4$，$d=\frac{4}{40}=0.1$，器乐考试中A等级的有3人
(2)“声乐”考试平均分为$(3× 10+10× 8+15× 6+8× 4+4× 2)÷ 40=6$(分);
(3)声乐成绩为A等级的有3人，器乐成绩为A等级的有3人，本考场此次测试恰有2人两科均为A，不妨记为$A',A''$，将声乐成绩为A等级的另一人记为$a$，将器乐成绩为A等级的另一人记为$b$.在至少一科成绩为A的考生中随机抽取两人有$A',A''$;$A',a$;$A',b$;$A'',a$;$A'',b$;$a,b$六种情形，两科成绩均为A等级的有一种情形，所以概率为$\frac{1}{6}$.