第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 下面的图形是天气预报使用的图标,其中是中心对称图形的是(

A
)
答案:
A
2. 抛物线 $ y = - 3 x ^ { 2 } + 6 x + 2 $ 的对称轴是(
A.直线 $ x = 2 $
B.直线 $ x = - 2 $
C.直线 $ x = 1 $
D.直线 $ x = - 1 $
C
)A.直线 $ x = 2 $
B.直线 $ x = - 2 $
C.直线 $ x = 1 $
D.直线 $ x = - 1 $
答案:
C
3. 方程 $ x ^ { 2 } - x + 3 = 0 $ 的根的情况是(
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.只有一个实数根
C
)A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.只有一个实数根
答案:
C
4. 某钢铁厂计划今年第一季度一月份的总产量为 $ 500 \mathrm { t } $,三月份的总产量为 $ 720 \mathrm { t } $,若平均每月的增长率相同,则第一季度平均每月的增长率为(
A.$ 22 \% $
B.$ 20 \% $
C.$ 16.7 \% $
D.$ 21 \% $
B
)A.$ 22 \% $
B.$ 20 \% $
C.$ 16.7 \% $
D.$ 21 \% $
答案:
B
5. 如图,一块含 $ 30 ^ { \circ } $ 角的直角三角板 $ A B C $ 绕点 $ C $ 顺时针旋转到 $ \triangle A ^ { \prime } B ^ { \prime } C $ 的位置,当 $ B $,$ C $,$ A ^ { \prime } $ 在同一条直线上时,三角板 $ A B C $ 的旋转角度为(
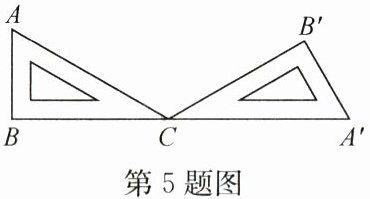
A.$ 150 ^ { \circ } $
B.$ 120 ^ { \circ } $
C.$ 60 ^ { \circ } $
D.$ 30 ^ { \circ } $
A
)
A.$ 150 ^ { \circ } $
B.$ 120 ^ { \circ } $
C.$ 60 ^ { \circ } $
D.$ 30 ^ { \circ } $
答案:
A
6. 蒙古包可近似地看作由圆锥和圆柱组成。若用毛毡搭建一个底面圆面积为 $ 16 \pi \mathrm { m } ^ { 2 } $,圆柱高为 $ 2 \mathrm { m } $,圆锥高为 $ 3 \mathrm { m } $ 的蒙古包,则需要毛毡的面积是( )
A.$ ( 24 + 4 \sqrt { 7 } ) \pi \mathrm { m } ^ { 2 } $
B.$ 44 \pi \mathrm { m } ^ { 2 } $
C.$ 36 \pi \mathrm { m } ^ { 2 } $
D.$ 48 \pi \mathrm { m } ^ { 2 } $
A.$ ( 24 + 4 \sqrt { 7 } ) \pi \mathrm { m } ^ { 2 } $
B.$ 44 \pi \mathrm { m } ^ { 2 } $
C.$ 36 \pi \mathrm { m } ^ { 2 } $
D.$ 48 \pi \mathrm { m } ^ { 2 } $
答案:
C 解析:如图所示,设圆柱底面圆的半径为r m。根据已知可得πr²=16π,
∴r = 4。
∴在Rt△AOB中,AB = 5 m,底面圆的周长C = 2πr = 8π m,
∴S_{扇}=$\frac{1}{2}$×8π×5 = 20π(m²),S_{矩}= 8π×2 = 16π(m²),
∴S_{总}= 36π m²。
C 解析:如图所示,设圆柱底面圆的半径为r m。根据已知可得πr²=16π,
∴r = 4。
∴在Rt△AOB中,AB = 5 m,底面圆的周长C = 2πr = 8π m,
∴S_{扇}=$\frac{1}{2}$×8π×5 = 20π(m²),S_{矩}= 8π×2 = 16π(m²),
∴S_{总}= 36π m²。

7. 欧几里得的《原本》记载,形如 $ x ^ { 2 } + a x = b ^ { 2 } $ 的方程的图解法:画 $ \mathrm { Rt } \triangle A B C $,使 $ \angle A C B = 90 ^ { \circ } $,$ B C = \frac { a } { 2 } $,$ A C = b $,再在斜边 $ A B $ 上截取 $ B D = \frac { a } { 2 } $。则该方程的一个正根是(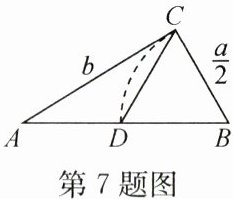
A.$ A C $ 的长
B.$ A D $ 的长
C.$ B C $ 的长
D.$ C D $ 的长
B
)
A.$ A C $ 的长
B.$ A D $ 的长
C.$ B C $ 的长
D.$ C D $ 的长
答案:
B 解析:设AD = x,根据勾股定理得(x + $\frac{a}{2}$)² = b² + ($\frac{a}{2}$)²,整理得x² + ax = b²,则该方程的一个正根是AD的长。
查看更多完整答案,请扫码查看


