《2025年提分教练九年级数学上册人教版》

15. (10 分)如图,一条公路的转弯处是一段圆弧 AB.
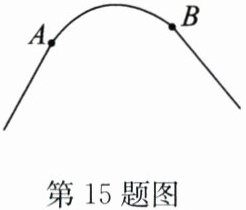
(1)作出$\overset{\frown}{AB}$所在圆的圆心 O；(用直尺和圆规作图,保留作图痕迹,不写作法)
(2)若$\overset{\frown}{AB}$的中点 C 到弦 AB 的距离为 20 m,AB = 80 m,求$\overset{\frown}{AB}$所在圆的半径.

答案：

(1)如图①.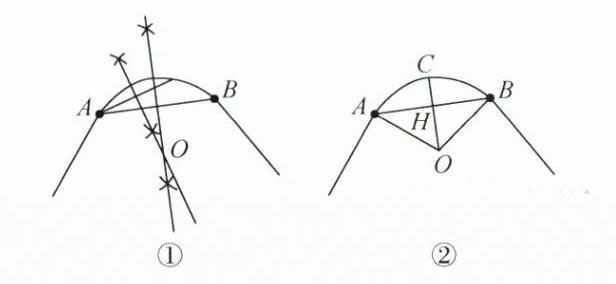
(2)如图②.设$\overset{\frown}{AB}$所在圆的半径为rm,则AO=rm,OH=(r −20)m.
∵OC⊥AB,
∴AH=$\frac{1}{2}$AB=40m,
∴在Rt△AHO中,由勾股定理，得AH²+OH²=OA²,即40²+(r−20)²=r²,解得r=50.故$\overset{\frown}{AB}$所在圆的半径为50m.

16. (10 分)如图,四边形 ABCD 内接于⊙O,点 E 在对角线 AC 上,EC = BC = DC.
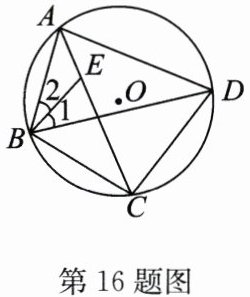
(1)若∠CBD = $39^{\circ}$,求∠BAD 的度数.
(2)求证：∠1 = ∠2.

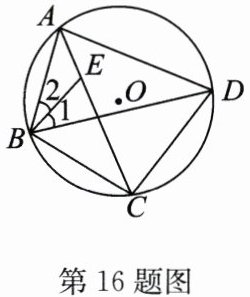
答案：
(1)解:
∵BC=DC,
∴∠CDB=∠CBD=39°.
∴∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°.
(2)证明:
∵EC=BC,
∴∠CEB=∠CBE;又
∵∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD.
∵∠BAE=∠CBD,
∴∠1=∠2.

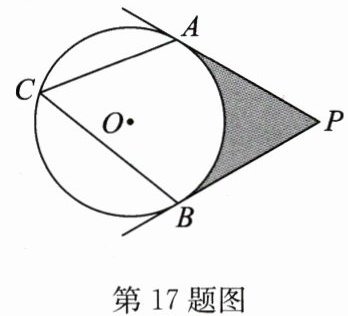
17. (10 分)如图,PA,PB 分别与⊙O 相切于 A,B 两点,∠ACB = $60^{\circ}$.
(1)求∠P 的度数；
(2)若⊙O 的半径为 4 cm,求图中阴影部分的面积.

答案：
(1)解:连接OA,OB,
∵PA,PB是⊙O的切线，
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°.
∵∠AOB=2∠C=120°,
∴∠APB=360°−(∠OAP+∠OBP +∠AOB)=360°−(90°+90°+120°)=60°.
(2)连接OP,
∵PA,PB是⊙O的切线，
∴∠APO=$\frac{1}{2}$∠APB=30°.
∴OP=2OA=8cm,
∴AP= $\sqrt{OP²−OA²}$=4$\sqrt{3}$cm.
∴S阴影=2S△AOP−S扇形AOB=2×$\frac{1}{2}$×4×4$\sqrt{3}$−$\frac{120π×4²}{360}$=(16$\sqrt{3}$ - $\frac{16π}{3}$)(cm²).

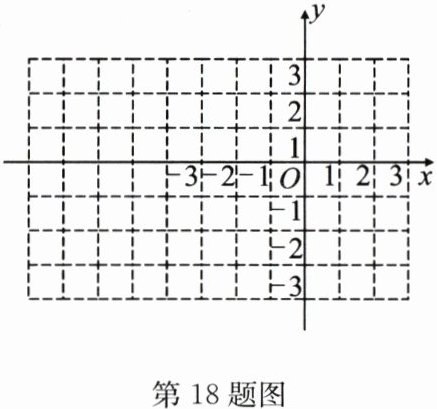
18. (10 分)在同一平面直角坐标系中有 5 个点：A(1,1),B(－3,－1),C(－3,1),D(－2,－2),E(0,－3).
(1)在图中画出△ABC 的外接圆⊙P,并指出点 D 与⊙P 的位置关系；
(2)若直线 l 经过点 D,E,判断直线 l 与⊙P 的位置关系.

答案：

(1)所画⊙P如图，由图可知，⊙P的半径为 $\sqrt{5}$ 连接PD,由题易得PD= $\sqrt{1²+2²}$=$\sqrt{5}$,
∴点D在⊙P上.
(2)如图,连接PE.由题易得PE²=1²+3²=10,PD²=5,DE²=5.
∴PE²=PD²+DE².
∴△PDE是直角三角形，且∠PDE=90°.
∵直线l过点D(−2,−2),E(0,−3),
∴PD⊥直线l.
∴直线l与⊙P相切.