第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
19. (12 分)已知抛物线 $ y = -x^{2}+bx + c $ 经过点 $ A(4,0) $ 和点 $ B(0,2) $,顶点为 $ C $。
(1) 求抛物线的解析式;
(2) 若抛物线的对称轴 $ l $ 与 $ x $ 轴交于点 $ D $,连接 $ AC $,$ BC $,$ BD $,求四边形 $ ADBC $ 的面积。
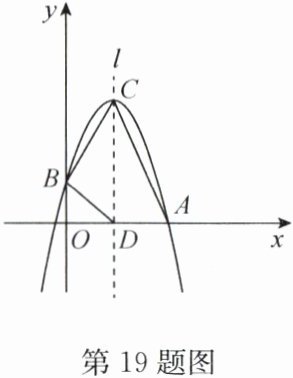
(1) 求抛物线的解析式;
(2) 若抛物线的对称轴 $ l $ 与 $ x $ 轴交于点 $ D $,连接 $ AC $,$ BC $,$ BD $,求四边形 $ ADBC $ 的面积。

答案:
解:
(1)$\because$抛物线$y=-x^{2}+bx+c$经过点$A(4,0)$,$B(0,2)$,$\therefore \begin{cases} -16+4b+c=0, \\c=2, \end{cases}$解得$\begin{cases} b=\dfrac{7}{2}, \\c=2, \end{cases}$
∴抛物线的解析式为$y=-x^{2}+\dfrac{7}{2}x+2$.
(2)$y=-x^{2}+\dfrac{7}{2}x+2=-\left(x-\dfrac{7}{4}\right)^{2}+\dfrac{81}{16}$,
∴$C\left(\dfrac{7}{4},\dfrac{81}{16}\right)$,
∴$S_{四边形ADBC}=S_{\triangle BOC}+S_{\triangle ADC}=\dfrac{1}{2}×4×\dfrac{81}{16}=\dfrac{81}{8}$.
(1)$\because$抛物线$y=-x^{2}+bx+c$经过点$A(4,0)$,$B(0,2)$,$\therefore \begin{cases} -16+4b+c=0, \\c=2, \end{cases}$解得$\begin{cases} b=\dfrac{7}{2}, \\c=2, \end{cases}$
∴抛物线的解析式为$y=-x^{2}+\dfrac{7}{2}x+2$.
(2)$y=-x^{2}+\dfrac{7}{2}x+2=-\left(x-\dfrac{7}{4}\right)^{2}+\dfrac{81}{16}$,
∴$C\left(\dfrac{7}{4},\dfrac{81}{16}\right)$,
∴$S_{四边形ADBC}=S_{\triangle BOC}+S_{\triangle ADC}=\dfrac{1}{2}×4×\dfrac{81}{16}=\dfrac{81}{8}$.
20. (12 分)随着粤港澳大湾区建设的加速推进,广东省正加速布局以 5G 等为代表的战略性新兴产业,某次统计时,广东 5G 基站的数量约 1.5 万座,到 2020 年底,全省 5G 基站数量是统计时的 4 倍,到 2022 年底,全省 5G 基站数量达到 17.34 万座。
(1) 到 2020 年底,全省 5G 基站的数量是多少万座?
(2) 求 2020 年底到 2022 年底,全省 5G 基站数量的年平均增长率。
(1) 到 2020 年底,全省 5G 基站的数量是多少万座?
(2) 求 2020 年底到 2022 年底,全省 5G 基站数量的年平均增长率。
答案:
解:
(1)由题意可得,到2020年底,全省5G基站的数量是$1.5×4=6$(万座).答:到2020年底,全省5G基站的数量是6万座.
(2)设年平均增长率为$x$,由题意可得$6(1+x)^{2}=17.34$,解得$x_{1}=0.7=70\%$,$x_{2}=-2.7$(舍去).答:2020年底到2022年底,全省5G基站数量的年平均增长率为70%.
(1)由题意可得,到2020年底,全省5G基站的数量是$1.5×4=6$(万座).答:到2020年底,全省5G基站的数量是6万座.
(2)设年平均增长率为$x$,由题意可得$6(1+x)^{2}=17.34$,解得$x_{1}=0.7=70\%$,$x_{2}=-2.7$(舍去).答:2020年底到2022年底,全省5G基站数量的年平均增长率为70%.
21. (15 分)如图,抛物线 $ y = x^{2}+bx + c $ 交 $ x $ 轴于 $ A(-1,0) $,$ B(3,0) $ 两点,交 $ y $ 轴于点 $ C $,其顶点为 $ D $,连接 $ BC $,点 $ P $ 从 $ A $ 点出发,在线段 $ AB $ 上以每秒 1 个单位长度的速度向 $ B $ 点运动,同时,点 $ Q $ 从 $ B $ 点出发,在线段 $ BC $ 上以每秒 $ \sqrt{2} $ 个单位长度的速度向 $ C $ 点运动,当其中一个点到达终点时,另一个点也停止运动,设运动时间为 $ t $ 秒。
(1) 求抛物线的解析式和顶点 $ D $ 的坐标。
(2) 点 $ Q $ 运动到何处时,点 $ Q $ 到点 $ D $,$ P $ 的距离相等?求出相应的点 $ Q $ 的坐标。
(3) 是否存在 $ t $,使得 $ \triangle BPQ $ 是等腰三角形?若存在,直接写出此时 $ t $ 的值;若不存在,请说明理由。
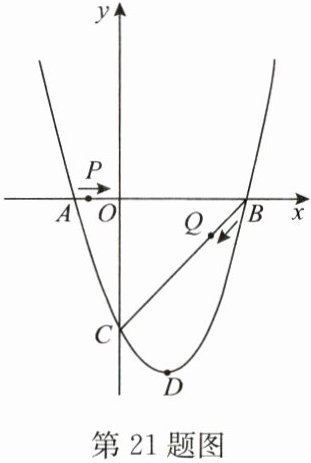
(1) 求抛物线的解析式和顶点 $ D $ 的坐标。
(2) 点 $ Q $ 运动到何处时,点 $ Q $ 到点 $ D $,$ P $ 的距离相等?求出相应的点 $ Q $ 的坐标。
(3) 是否存在 $ t $,使得 $ \triangle BPQ $ 是等腰三角形?若存在,直接写出此时 $ t $ 的值;若不存在,请说明理由。

答案:
解:
(1)把$A(-1,0)$,$B(3,0)$分别代入抛物线的解析式,得$\begin{cases} 0=1-b+c, \\0=9+3b+c, \end{cases}$解得$\begin{cases} b=-2, \\c=-3, \end{cases}$
∴抛物线的解析式为$y=x^{2}-2x-3$.$\because y=x^{2}-2x-3=(x-1)^{2}-4$,
∴顶点$D$的坐标为$(1,-4)$.
(2)由
(1)可知点$C(0,-3)$,$D(1,-4)$.又$\because B(3,0)$,
∴$OB=OC=3$.设当点$P、Q$的运动时间为$t$秒时,有$QD=QP$,则点$P$的坐标为$(t-1,0)$,$BQ=\sqrt{2}t$.$\because OB=OC$,
∴$\triangle OBC$为等腰直角三角形,
∴点$Q$的坐标为$(3-t,-t)$.$\therefore PQ^{2}=[3-t-(t-1)]^{2}+(-t)^{2}=5t^{2}-16t+16$,$DQ^{2}=(3-t-1)^{2}+[(-t)-(-4)]^{2}=2t^{2}-12t+20$.$\because QD=QP$,$\therefore 5t^{2}-16t+16=2t^{2}-12t+20$,解得$t=2$或$t=-\dfrac{2}{3}$(舍去),
∴当$t=2$时,$QD=QP$,此时点$Q$的坐标为$(1,-2)$.
(3)存在$t$,使得$\triangle BPQ$为等腰三角形.由
(2)可知$BP=4-t$,$BQ=\sqrt{2}t$,$PQ=\sqrt{5t^{2}-16t+16}$.①当$BP=BQ$时,$4-t=\sqrt{2}t$,解得$t=4\sqrt{2}-4$.②当$BQ=PQ$时,$\sqrt{2}t=\sqrt{5t^{2}-16t+16}$,解得$t=\dfrac{4}{3}$或$t=4$(舍去).③当$PQ=PB$时,$\sqrt{5t^{2}-16t+16}=4-t$,解得$t=2$或$t=0$(舍去).综上,当$t$的值为$4\sqrt{2}-4$或$\dfrac{4}{3}$或2时,$\triangle BPQ$为等腰三角形.
(1)把$A(-1,0)$,$B(3,0)$分别代入抛物线的解析式,得$\begin{cases} 0=1-b+c, \\0=9+3b+c, \end{cases}$解得$\begin{cases} b=-2, \\c=-3, \end{cases}$
∴抛物线的解析式为$y=x^{2}-2x-3$.$\because y=x^{2}-2x-3=(x-1)^{2}-4$,
∴顶点$D$的坐标为$(1,-4)$.
(2)由
(1)可知点$C(0,-3)$,$D(1,-4)$.又$\because B(3,0)$,
∴$OB=OC=3$.设当点$P、Q$的运动时间为$t$秒时,有$QD=QP$,则点$P$的坐标为$(t-1,0)$,$BQ=\sqrt{2}t$.$\because OB=OC$,
∴$\triangle OBC$为等腰直角三角形,
∴点$Q$的坐标为$(3-t,-t)$.$\therefore PQ^{2}=[3-t-(t-1)]^{2}+(-t)^{2}=5t^{2}-16t+16$,$DQ^{2}=(3-t-1)^{2}+[(-t)-(-4)]^{2}=2t^{2}-12t+20$.$\because QD=QP$,$\therefore 5t^{2}-16t+16=2t^{2}-12t+20$,解得$t=2$或$t=-\dfrac{2}{3}$(舍去),
∴当$t=2$时,$QD=QP$,此时点$Q$的坐标为$(1,-2)$.
(3)存在$t$,使得$\triangle BPQ$为等腰三角形.由
(2)可知$BP=4-t$,$BQ=\sqrt{2}t$,$PQ=\sqrt{5t^{2}-16t+16}$.①当$BP=BQ$时,$4-t=\sqrt{2}t$,解得$t=4\sqrt{2}-4$.②当$BQ=PQ$时,$\sqrt{2}t=\sqrt{5t^{2}-16t+16}$,解得$t=\dfrac{4}{3}$或$t=4$(舍去).③当$PQ=PB$时,$\sqrt{5t^{2}-16t+16}=4-t$,解得$t=2$或$t=0$(舍去).综上,当$t$的值为$4\sqrt{2}-4$或$\dfrac{4}{3}$或2时,$\triangle BPQ$为等腰三角形.
查看更多完整答案,请扫码查看


