《2025年提分教练九年级数学上册人教版》

15. (10 分)已知抛物线的顶点坐标为 $ ( - 1, - 3 ) $,与 $ y $ 轴的交点为 $ ( 0, - 5 ) $。
(1)求抛物线对应的函数解析式。
(2)将上面的抛物线向右平移 2 个单位长度,再向上平移 3 个单位长度会得到怎样的抛物线？
(3)若(2)中所求抛物线的顶点不动,且抛物线的开口方向相反,求符合此条件的抛物线对应的函数解析式。

答案：
(1)根据题意设$y=a(x+1)^2-3(a\neq0)$，
　将$(0,-5)$代入，得$a-3=-5$，解得$a=-2$.
∴抛物线对应的函数解析式为$y=-2(x+1)^2-3=-2x^2-4x-5$.
(2)原抛物线的顶点坐标为$(-1,-3)$，先向右平移2个单位长度，再向上平移3个单位长度后，得到新抛物线的顶点坐标为$(1,0)$.
　故新抛物线对应的函数解析式为$y=-2(x-1)^2$.
(3)所求的抛物线对应的函数解析式为$y=2(x-1)^2$.

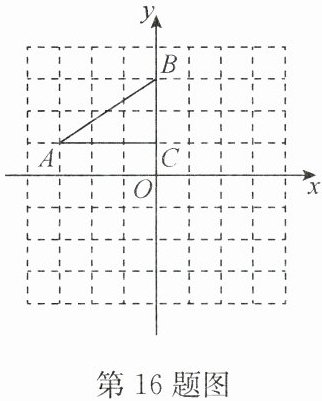
16. (10 分)如图,在平面直角坐标系中,$ \mathrm { Rt } \triangle ABC $ 的三个顶点分别是 $ A ( - 3, 1 ) $,$ B ( 0, 3 ) $,$ C ( 0, 1 ) $。
(1)将 $ \triangle ABC $ 以点 $ C $ 为旋转中心旋转 $ 180 ^ { \circ } $,画出旋转后对应的 $ \triangle A _ { 1 } B _ { 1 } C $；
(2)分别连接 $ AB _ { 1 } $,$ BA _ { 1 } $ 后,求四边形 $ AB _ { 1 } A _ { 1 } B $ 的面积。

答案：

(1)如图，$\triangle A_1B_1C$为所作
　　　　　　　　
(2)易证四边形$AB_1A_1B$为菱形，
∴四边形$AB_1A_1B$的面积$=\frac{1}{2}×6×4=12$.

17. (10 分)已知 $ k ＞ 0 $,且关于 $ x $ 的方程 $ 3 k x ^ { 2 } + 12 x + k + 1 = 0 $ 有两个相等的实数根。
(1)求 $ k $ 的值；
(2)求出这两个实数根。

答案：
(1)由题意得，$\Delta=12^2-4×3k×(k+1)=144-12k^2-12k=0$，解得$k_1=3$，$k_2=-4$(舍).
(2)当$k=3$时，$9x^2+12x+4=0$，整理得$(3x+2)^2=0$，解得$x_1=x_2=-\frac{2}{3}$.

18. (10 分)电动自行车已成为市民日常出行的首选工具。据某市某品牌电动自行车经销商 1 至 3 月份统计,该品牌电动自行车 1 月份销售 150 辆,3 月份销售 216 辆。
(1)求该品牌电动自行车销售量的月均增长率。
(2)若该品牌电动自行车的进价为 2 300 元/辆,售价为 2 800 元/辆,则该经销商 1 至 3 月份共盈利多少元？

答案：
(1)设该品牌电动自行车销售量的月均增长率为$x$，
　根据题意列方程为$150(1+x)^2=216$，
　解得$x_1=-220\%$(不合题意，舍去)，$x_2=20\%$，
　故该品牌电动自行车销售量的月均增长率为$20\%$.
(2)2月份的销量是$150×(1+20\%)=180$(辆).
　所以该经销商1至3月份共盈利$(2800-2300)×(150+180+216)=500×546=273000$(元).