《2025年提分教练九年级数学上册人教版》

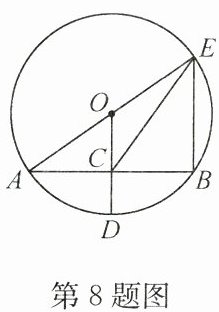
8. 如图,$\odot O$ 的半径 $OD$ 垂直于弦 $AB$,垂足为点 $C$,连接 $AO$ 并延长交$\odot O$于点 $E$,连接 $BE$,$CE$。若 $AB = 8$,$CD = 2$,则$\triangle BCE$的面积为(12)

A.$12$
B.$15$
C.$16$
D.$18$

答案： A　解析:
∵⊙O的半径OD垂直于弦AB，垂足为点C,AB=8,
∴AC=BC=$\frac{1}{2}$AB=4.设OA=r,则OC=r−2,在Rt△AOC中，
∵AC²+OC²=OA²,即4²+(r−2)²=r²,解得r=5,
∴AE=10,
∴BE= $\sqrt{AE^{2}-AB^{2}}$=$\sqrt{10^{2}-8^{2}}$=6,
∴△BCE的面积=$\frac{1}{2}$BC·BE=$\frac{1}{2}$×4×6=12.

9. 当 $x$ 的值为4或−2时,代数式 $2x^{2}-4x$ 与代数式 $x^{2}-2x + 8$ 的值相等。

答案： 4或−2　解析:由题意得2x²−4x=x²−2x+8,化简得x²−2x−8=0,变形得(x−4)(x+2)=0,即x−4=0或x+2=0,解得x₁=4,x₂=−2,故当x=4或x=−2时，两个代数式的值相等.

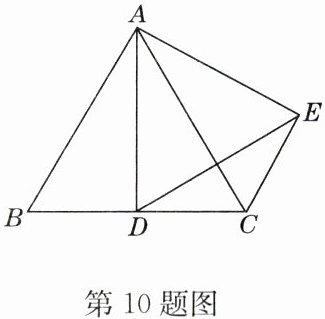
10. 如图,在等边$\triangle ABC$中,$AB = 6$,$D$ 是 $BC$ 的中点,将$\triangle ABD$绕点 $A$ 旋转后得到$\triangle ACE$,那么线段 $DE$ 的长度为3$\sqrt{3}$。

答案： 3$\sqrt{3}$

11. 已知二次函数的图象与 $x$ 轴交于 $A(-2,0)$、$B(3,0)$ 两点,且函数有最大值 $2$,则该二次函数的解析式为y=−$\frac{8}{25}$(x+2)(x−3)。

答案： y=−$\frac{8}{25}$(x+2)(x−3)　解析:由题可设函数的解析式为y=a(x+2)(x−3)(a≠0),整理得y=a(x−$\frac{1}{2}$)²−$\frac{25}{4}$a(a≠0),
∵函数有最大值2,
∴−$\frac{25}{4}$a=2,解得a=−$\frac{8}{25}$，符合题意，
∴二次函数的解析式为y=−$\frac{8}{25}$(x+2)(x−3).

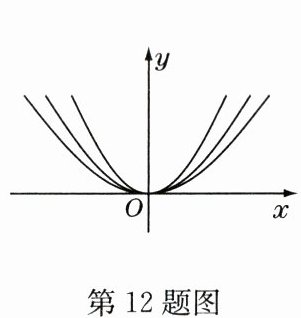
12. 如图所示,在同一平面直角坐标系中,作出①$y = 3x^{2}$,②$y= \frac{1}{2}x^{2}$,③$y = x^{2}$ 的图象,则图中从里到外的三条抛物线对应的函数依次是①③②(填序号)。

答案： ①③②

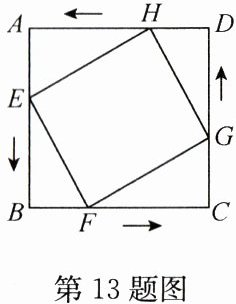
13. 如图,在边长为 $6$ 的正方形 $ABCD$ 中,点 $E$、$F$、$G$、$H$ 分别从点 $A$、$B$、$C$、$D$ 同时出发,均以每秒 $1$ 个单位长度的速度向点 $B$、$C$、$D$、$A$ 匀速运动,当点 $E$ 到达点 $B$ 时,四个点同时停止运动,在运动过程中,当运动时间为3$s$ 时,四边 $EFGH$ 的面积最小,其最小值是18。

答案： 3　18　解析:设运动时间为t(0≤t≤6),则AE=t,AH=6−t,根据题意得S四边形EFGH=S正方形ABCD−4S△AEH=6×6−4×$\frac{1}{2}$t(6−t)=2t²−12t+36=2(t−3)²+18,
∴当t=3时，四边形EFGH的面积取得最小值，最小值为18.

14. (10 分)用适当方法解下列方程：
(1)$x^{2}+4x - 3 = 0$；
(2)$(x + 3)^{2}= (2x - 1)^{2}$。

答案： $(1)$ 解方程$x^{2}+4x - 3 = 0$
解：对于一元二次方程$ax^{2}+bx + c = 0$（$a\neq0$），其求根公式为$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$。
在方程$x^{2}+4x - 3 = 0$中，$a = 1$，$b = 4$，$c = -3$。
先计算判别式$\Delta=b^{2}-4ac$，将$a = 1$，$b = 4$，$c = -3$代入可得：
$\Delta = 4^{2}-4×1×(-3)$
$=16 + 12$
$=28$
再将$a$、$b$、$\Delta$的值代入求根公式可得：
$x=\frac{-4\pm\sqrt{28}}{2×1}=\frac{-4\pm2\sqrt{7}}{2}=-2\pm\sqrt{7}$
所以方程$x^{2}+4x - 3 = 0$的解为$x_{1}=-2+\sqrt{7}$，$x_{2}=-2-\sqrt{7}$。
$(2)$ 解方程$(x + 3)^{2}= (2x - 1)^{2}$
解：
方法一：直接开方法
对$(x + 3)^{2}= (2x - 1)^{2}$两边同时开平方得：
$x + 3=\pm(2x - 1)$
当$x + 3 = 2x - 1$时，
移项可得：$3 + 1 = 2x - x$，
解得$x = 4$。
当$x + 3 = -(2x - 1)$时，
去括号得$x + 3 = -2x + 1$，
移项可得：$x + 2x = 1 - 3$，
合并同类项得$3x = -2$，
解得$x=-\frac{2}{3}$。
方法二：因式分解法
将$(x + 3)^{2}-(2x - 1)^{2}=0$，根据平方差公式$a^{2}-b^{2}=(a + b)(a - b)$，这里$a=x + 3$，$b = 2x - 1$，则有：
$[(x + 3)+(2x - 1)][(x + 3)-(2x - 1)] = 0$
即$(3x + 2)(-x + 4)=0$
所以$3x + 2 = 0$或$-x + 4 = 0$
当$3x + 2 = 0$时，$3x=-2$，解得$x = -\frac{2}{3}$；
当$-x + 4 = 0$时，解得$x = 4$。
综上，方程$(x + 3)^{2}= (2x - 1)^{2}$的解为$x_{1}=4$，$x_{2}=-\frac{2}{3}$。

15. (10 分)若一个三角形的三边长满足方程 $x^{2}-3x + 2 = 0$,求此三角形的周长。

答案： 解:解方程x²−3x+2=0可得x₁=1,x₂=2.因为三角形三个边长均为此方程的根，所以三角形的三边长度可分为以下几种情况:①三边长为1,1,1,此时三角形的周长为3;②三边长为2,2,2,此时三角形的周长为6;③三边长为1,2,2，此时三角形的周长为5;④三边长为1,1,2，此时无法构成三角形(舍去).综上，此三角形的周长为3或5或6.