《2025年提分教练九年级数学上册人教版》

7. 如图,在平面直角坐标系 $ xOy $ 中,抛物线 $ y = - 2 x ^ { 2 } + m x + n $ 与 $ x $ 轴交于 $ A $,$ B $ 两点。若顶点 $ C $ 到 $ x $ 轴的距离为 8,则线段 $ AB $ 的长度为(D)

A.2
B.$ 2 \sqrt { 2 } $
C.$ \sqrt { 15 } $
D.4

答案： D　解析:设抛物线解析式为$y=-2(x-h)^2+8$.当$y=0$时，$-2(x-h)^2+8=0$，解得$x_1=h-2$，$x_2=h+2$，所以$A(h-2,0)$，$B(h+2,0)$，所以$AB=h+2-(h-2)=4$.故选D.

8. 已知二次函数 $ y = a x ^ { 2 } + b x + c ( a \neq 0 ) $ 的图象如图,有下列结论：① $ b ^ { 2 } - 4 a c ＞ 0 $；② $ a b c ＞ 0 $；③ $ 8 a + c ＞ 0 $；④ $ 6 a + 3 b + c ＞ 0 $。其中正确结论的个数是(B)

A.4
B.3
C.2
D.1

答案： B

9. 将一元二次方程 $ x ^ { 2 } + 8 x + 3 = 0 $ 化成 $ ( x + a ) ^ { 2 } = b $ 的形式,则 $ a + b $ 的值为17。

答案： 17

10. 把方程 $ x ^ { 2 } - 3 = 2 x $ 用配方法化为 $ ( x + m ) ^ { 2 } = n $ 的形式,则 $ m = $-1,$ n = $4。

答案： -1　4

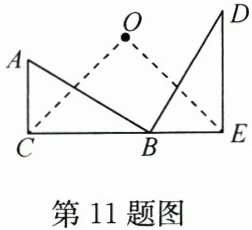
11. 如图,将 $ \mathrm { Rt } \triangle ABC $ 绕 $ O $ 点旋转 $ 90 ^ { \circ } $,得 $ \mathrm { Rt } \triangle BDE $,其中 $ \angle ACB = \angle BED = 90 ^ { \circ } $,$ AC = 6 $,$ AB = 10 $,则点 $ C $ 与旋转中心点 $ O $ 的距离 $ OC $ 的长是______。

答案：
$7\sqrt{2}$　解析:如图，
∵$\angle ACB=90°$，$AC=6$，$AB=10$，
∴$BC=\sqrt{AB^2-AC^2}=8$.
∵将$Rt\triangle ABC$绕$O$点旋转$90°$得到$Rt\triangle BDE$，
∴$BE=AC=6$，$OC=OE$，$\angle COE=90°$，
∴$\triangle OCE$为等腰直角三角形，
∴$OC=\frac{\sqrt{2}}{2}CE=\frac{\sqrt{2}}{2}×(8+6)=7\sqrt{2}$.
　　　　　　　　　　　　　　　　　

12. 若关于 $ x $ 的一元二次方程 $ x ^ { 2 } - 5 x + k = 0 $ 有两个不相等的实数根,则 $ k $ 可取的最大整数为6。

答案： 6

13. 如图,在喷水池的中心 $ A $ 处竖直安装一根水管 $ AB $,水管的顶端安有一个喷水头,使喷出的抛物线形水柱在与池中心 $ A $ 的水平距离为 1 m 处达到最高点 $ C $,高度为 3 m,水柱落地点 $ D $ 离池中心 $ A $ 处 3 m,以水平方向为 $ x $ 轴,建立平面直角坐标系。若选取点 $ A $ 为坐标原点时的抛物线的解析式为 $ y = - \frac { 3 } { 4 } ( x - 1 ) ^ { 2 } + 3 ( 0 \leq x \leq 3 ) $,则选取点 $ D $ 为坐标原点时的抛物线解析式为$y=-\frac{3}{4}(x+2)^2+3$,水管 $ AB $ 的长为2.25m。

答案： $y=-\frac{3}{4}(x+2)^2+3$　2.25　解析:以喷水池的中心$A$为原点建立平面直角坐标系，抛物线的解析式为$y=-\frac{3}{4}(x-1)^2+3$.当选取点$D$为坐标原点时，相当于将原图象向左平移3个单位长度，故平移后的抛物线解析式为$y=-\frac{3}{4}(x+2)^2+3$($-3\leqslant x\leqslant0$).
　令原抛物线解析式中$x=0$，则$y=\frac{9}{4}=2.25$.故水管$AB$的长为$2.25$m.

14. (10 分)运用适当的方法解方程。
(1)$ 4 x ^ { 2 } - 6 x - 3 = 0 $；
(2)$ ( 2 x - 3 ) ^ { 2 } = 5 ( 2 x - 3 ) $。

答案：
(1)$4x^2-6x-3=0$，
∵$b^2-4ac=(-6)^2-4×4×(-3)=84$，
∴$x=\frac{6\pm\sqrt{84}}{2×4}=\frac{3\pm\sqrt{21}}{4}$，
∴$x_1=\frac{3+\sqrt{21}}{4}$，$x_2=\frac{3-\sqrt{21}}{4}$.
(2)$(2x-3)^2=5(2x-3)$，
　移项，得$(2x-3)^2-5(2x-3)=0$.
　因式分解，得$(2x-3)(2x-3-5)=0$.
∴$2x-3=0$或$2x-3-5=0$，
∴$x_1=\frac{3}{2}$，$x_2=4$.