《2025年提分教练九年级数学上册人教版》

7. 如图,在梯形 $ ABCD $ 中,$ AB // CD $,对角线 $ AC $、$ BD $ 相交于点 $ O $,有下面四个结论：① $ \triangle AOB \sim \triangle COD $；② $ \triangle AOD \sim \triangle BOC $；③ $ S_{\triangle DOC} : S_{\triangle BOA} = DC : AB $；④ $ S_{\triangle AOD} = S_{\triangle BOC} $。其中正确的有(B)

A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个

答案： B

8. 如图,矩形 $ OABC $ 与矩形 $ ODEF $ 是位似图形,点 $ O $ 为位似中心,相似比为 $ 1 : 1.2 $,点 $ B $ 的坐标为 $ (-3, 2) $,则点 $ E $ 的坐标是(D)

A.$ (3.6, 2.4) $
B.$ (-3, 2.4) $
C.$ (-3.6, 2) $
D.$ (-3.6, 2.4) $

答案： D

9. 如图,在 $ \triangle ABC $ 中,$ DE // BC $,分别交 $ AB $、$ AC $ 于点 $ D $、$ E $,若 $ AD = 3 $,$ DB = 2 $,$ BC = 6 $,则 $ DE $ 的长为$\frac{18}{5}$。

答案： $\frac{18}{5}$

10. 已知两相似三角形的面积比为 $ 1 : 4 $,则它们的对应中线长的比为1:2。

答案： 1:2

11. 如图,测量小玻璃管口径的量具 $ ABC $ 上,$ AB $ 的长为 $ 10 $ 毫米,$ AC $ 被分为 $ 60 $ 等份,如果小管口中 $ DE $ 正好对着量具上 $ 20 $ 份处($ DE // AB $),那么小管口径 $ DE $ 的长是$\frac{10}{3}$毫米。

答案： $\frac{10}{3}$

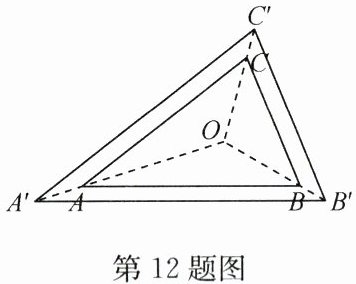
12. 如图,$ \triangle ABC $ 与 $ \triangle A'B'C' $ 是位似图形,点 $ O $ 是位似中心,若 $ OA = 3AA' $,$ S_{\triangle ABC} = 9 $,则 $ S_{\triangle A'B'C'} = $16。

答案： 16

13. 如图,在矩形 $ ABCD $ 中,$ AD = 2 $,$ AB = 5 $,$ P $ 为 $ CD $ 边上的动点,当 $ \triangle ADP $ 与 $ \triangle BCP $ 相似时,$ DP = $1或4或2.5。

答案： 1或4或2.5　解析:①当△APD∽△PBC时，则$\frac{AD}{PC}=\frac{PD}{BC}$，即$\frac{2}{5 - PD}=\frac{PD}{2}$，解得PD = 1或PD = 4。②当△PAD∽△PBC时，$\frac{AD}{BC}=\frac{PD}{PC}$，即$\frac{2}{2}=\frac{PD}{5 - PD}$，解得PD = 2.5。综上所述，PD的长度是1或4或2.5。

14. (10 分)如图,四边形 $ ABCD $ 与四边形 $ A'B'C'D' $ 是相似图形,点 $ A $ 与点 $ A' $、点 $ B $ 与点 $ B' $、点 $ C $ 与点 $ C' $、点 $ D $ 与点 $ D' $ 分别是对应顶点,已知数据如图所示,求未知边 $ x $、$ y $ 的长度和角 $ \alpha $、$ \beta $ 的大小。

答案： 解:
∵四边形ABCD∽四边形A'B'C'D'，
∴∠D' = β = ∠D = 55°，∠B = ∠B' = 60°，∠A = α = 360° - 55° - 90° - 60° = 155°。
∴$\frac{9}{x}=\frac{12}{8}=\frac{y}{10}$，
∴x = 6，y = 15。