第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
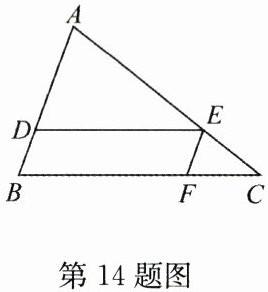
14. (10 分)如图,已知在 $ \triangle ABC $ 中,$ DE // BC $,$ EF // AB $,$ AE = 2CE $,$ AB = 6 $,$ BC = 9 $. 求:
(1)$ BF $ 和 $ BD $ 的长度;
(2)四边形 $ BDEF $ 的周长.
(1)$ BF $ 和 $ BD $ 的长度;
(2)四边形 $ BDEF $ 的周长.

答案:
解:
(1)
∵AE=2CE,
∴$\frac{CE}{AE}=\frac{1}{2}$.
∵EF//AB,
∴$\frac{AE}{AC}=\frac{BF}{BC}=\frac{2}{3}$.
∵BC=9,
∴BF=6.
∵DE//BC,
∴$\frac{BD}{AB}=\frac{CE}{AC}=\frac{1}{3}$.
∵AB=6,
∴BD=2.
(2)
∵EF//AB,DE//BC,
∴四边形BDEF是平行四边形,
∴BD=EF=2,DE=BF=6,
∴四边形BDEF的周长为2×(2+6)=16.
(1)
∵AE=2CE,
∴$\frac{CE}{AE}=\frac{1}{2}$.
∵EF//AB,
∴$\frac{AE}{AC}=\frac{BF}{BC}=\frac{2}{3}$.
∵BC=9,
∴BF=6.
∵DE//BC,
∴$\frac{BD}{AB}=\frac{CE}{AC}=\frac{1}{3}$.
∵AB=6,
∴BD=2.
(2)
∵EF//AB,DE//BC,
∴四边形BDEF是平行四边形,
∴BD=EF=2,DE=BF=6,
∴四边形BDEF的周长为2×(2+6)=16.
15. (10 分)如图,已知 $ \triangle ABC $ 的三个顶点坐标如下表.
(1)将下表补充完整,并在直角坐标系中画出 $ \triangle A{'}B{'}C{'} $;
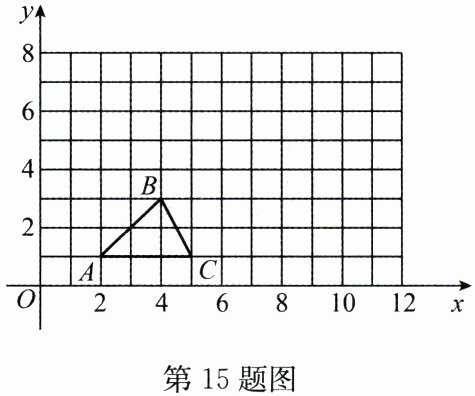

(2)观察两个三角形,可知 $ \triangle ABC \sim \triangle A{'}B{'}C{'} $,两个三角形是以原点为位似中心的位似三角形,$ \triangle ABC $ 与 $ \triangle A{'}B{'}C{'} $ 的相似比为______.
(1)将下表补充完整,并在直角坐标系中画出 $ \triangle A{'}B{'}C{'} $;


(2)观察两个三角形,可知 $ \triangle ABC \sim \triangle A{'}B{'}C{'} $,两个三角形是以原点为位似中心的位似三角形,$ \triangle ABC $ 与 $ \triangle A{'}B{'}C{'} $ 的相似比为______.
答案:
解:
(1)B'(8,6),C'(10,2).
如图所示,△A'B'C'即为所求.

(2)△ABC与△A'B'C'的相似比为1:2.
解:
(1)B'(8,6),C'(10,2).
如图所示,△A'B'C'即为所求.

(2)△ABC与△A'B'C'的相似比为1:2.
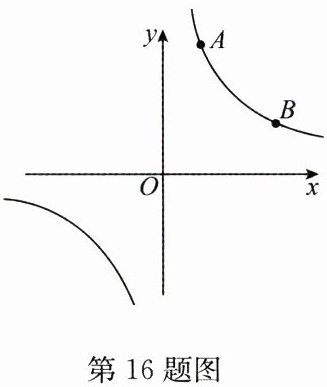
16. (10 分)反比例函数 $ y = \frac{k}{x} $($ k $ 为常数,且 $ k \neq 0 $)的图象经过点 $ A(1,3) $,$ B(3,m) $.
(1)求反比例函数的解析式及 $ B $ 点的坐标;
(2)在 $ x $ 轴上找一点 $ P $,使 $ PA + PB $ 的值最小,求满足条件的 $ P $ 点的坐标.
(1)求反比例函数的解析式及 $ B $ 点的坐标;
(2)在 $ x $ 轴上找一点 $ P $,使 $ PA + PB $ 的值最小,求满足条件的 $ P $ 点的坐标.

答案:
解:
(1)把A(1,3)的坐标代入$y=\frac{k}{x}$(k为常数,且k≠0),得k =1×3=3,
∴反比例函数的解析式为$y=\frac{3}{x}$.
把B(3,m)的坐标代入$y=\frac{3}{x}$,得3m=3,解得m=1,
∴B点坐标为(3,1).
(2)作A点关于x轴的对称点A',连接BA'交x轴于P点,连接AP,如图,则A'(1,−3).

此时PA+PB的值最小,为A'B的长度.
设直线BA'的解析式为y=mx+n(m≠0),把A'(1,−3),B(3,1)的坐标代入,
得$\begin{cases}m + n = -3\\3m + n = 1\end{cases}$,解得$\begin{cases}m = 2\\n = -5\end{cases}$,
∴直线BA'的解析式为y=2x−5.
当y=0时,2x−5=0,解得$x=\frac{5}{2}$,
∴点P的坐标为($\frac{5}{2}$,0).
解:
(1)把A(1,3)的坐标代入$y=\frac{k}{x}$(k为常数,且k≠0),得k =1×3=3,
∴反比例函数的解析式为$y=\frac{3}{x}$.
把B(3,m)的坐标代入$y=\frac{3}{x}$,得3m=3,解得m=1,
∴B点坐标为(3,1).
(2)作A点关于x轴的对称点A',连接BA'交x轴于P点,连接AP,如图,则A'(1,−3).

此时PA+PB的值最小,为A'B的长度.
设直线BA'的解析式为y=mx+n(m≠0),把A'(1,−3),B(3,1)的坐标代入,
得$\begin{cases}m + n = -3\\3m + n = 1\end{cases}$,解得$\begin{cases}m = 2\\n = -5\end{cases}$,
∴直线BA'的解析式为y=2x−5.
当y=0时,2x−5=0,解得$x=\frac{5}{2}$,
∴点P的坐标为($\frac{5}{2}$,0).
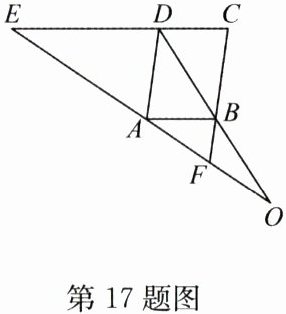
17. (10 分)如图,已知 $ EC // AB $,$ \angle EDA = \angle ABF $. 求证:
(1)四边形 $ ABCD $ 是平行四边形;
(2)$ OA^2 = OE \cdot OF $.
(1)四边形 $ ABCD $ 是平行四边形;
(2)$ OA^2 = OE \cdot OF $.

答案:
证明:
(1)
∵EC//AB,
∴∠EDA=∠DAB.
∵∠EDA=∠ABF,
∴∠DAB=∠ABF,
∴AD//BC.
∴四边形ABCD是平行四边形.
(2)
∵EC//AB,
∴△OAB∽△OED,
∴$\frac{OA}{OE}=\frac{OB}{OD}$.
∵AD//BC,
∴△OBF∽△ODA,
∴$\frac{OB}{OD}=\frac{OF}{OA}$,
∴$\frac{OA}{OE}=\frac{OF}{OA}$,
∴OA²=OE·OF.
(1)
∵EC//AB,
∴∠EDA=∠DAB.
∵∠EDA=∠ABF,
∴∠DAB=∠ABF,
∴AD//BC.
∴四边形ABCD是平行四边形.
(2)
∵EC//AB,
∴△OAB∽△OED,
∴$\frac{OA}{OE}=\frac{OB}{OD}$.
∵AD//BC,
∴△OBF∽△ODA,
∴$\frac{OB}{OD}=\frac{OF}{OA}$,
∴$\frac{OA}{OE}=\frac{OF}{OA}$,
∴OA²=OE·OF.
查看更多完整答案,请扫码查看


