第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
7. 如图,将 $ \triangle ABC $ 绕点 $ C(0,-1) $ 旋转 $ 180^{\circ} $ 得到 $ \triangle A'B'C $,设点 $ A' $ 的坐标为 $ (a,b) $,则点 $ A $ 的坐标为 (
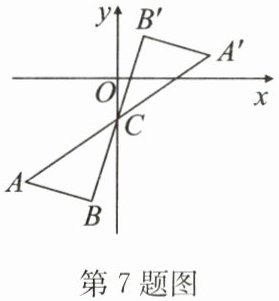
A.$ (-a,-b) $
B.$ (-a,-b - 1) $
C.$ (-a,-b + 1) $
D.$ (-a,-b - 2) $
D
)
A.$ (-a,-b) $
B.$ (-a,-b - 1) $
C.$ (-a,-b + 1) $
D.$ (-a,-b - 2) $
答案:
D
8. 如图,在 $ 4×4 $ 的正方形网格中,将图中的 2 个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有 (

A.7 个
B.8 个
C.9 个
D.10 个
D
)
A.7 个
B.8 个
C.9 个
D.10 个
答案:
D
9. 点 $ O $ 是正五边形 $ ABCDE $ 的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图). 这个图案绕点 $ O $ 至少旋转______$ ^{\circ} $ 后能与原来的图案互相重合.
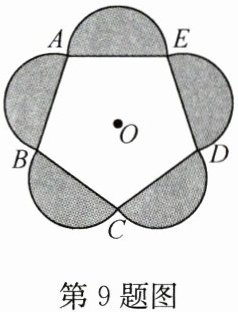

72
答案:
72
10. 如图,点 $ C $ 为线段 $ AB $ 上一点,将线段 $ CB $ 绕点 $ C $ 旋转,得到线段 $ CD $,若 $ DA \perp AB $,$ AD = 1 $,$ BD = \sqrt{17} $,则 $ BC $ 的长为
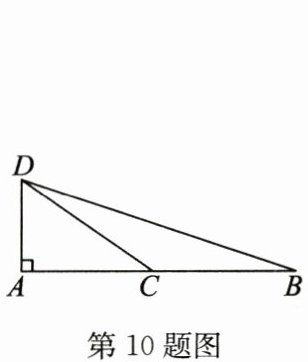
$\frac{17}{8}$
.
答案:
$\frac{17}{8}$
11. 如图,$ \triangle ABC $ 是等腰直角三角形,$ BC $ 是斜边,将 $ \triangle ABD $ 绕点 $ A $ 逆时针旋转后,能与 $ \triangle ACD' $ 重合. 如果 $ AD = 2 $,那么 $ DD' = $
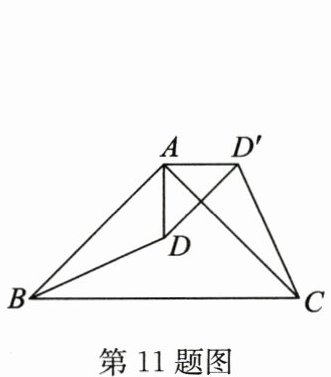
$2\sqrt{2}$
.
答案:
$2\sqrt{2}$
12. 如图,在平面直角坐标系中,点 $ P(1,1) $,$ N(2,0) $,$ \triangle MNP $ 和 $ \triangle M_1N_1P_1 $ 的顶点都在格点上,$ \triangle MNP $ 与 $ \triangle M_1N_1P_1 $ 关于某一点成中心对称,则对称中心的坐标为______.
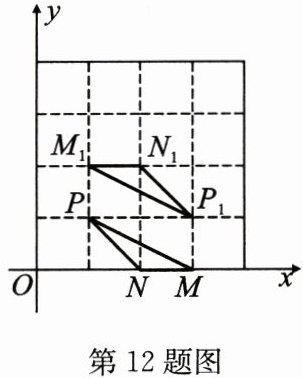

(2,1)
答案:
(2,1)
13. 如图,在 $ \triangle ABC $ 中,$ \angle BAC = 90^{\circ} $,$ AB = 2 $. 将 $ \triangle ABC $ 绕点 $ A $ 按顺时针方向旋转至 $ \triangle AB_1C_1 $ 的位置,点 $ B_1 $ 恰好落在边 $ BC $ 的中点处,则 $ CC_1 $ 的长为______.
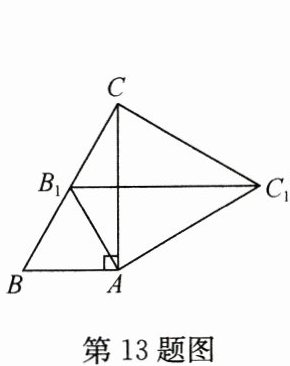

$2\sqrt{3}$
答案:
$2\sqrt{3}$ 解析:
∵在$\triangle ABC$中,$\angle BAC=90^{\circ}$,将$\triangle ABC$绕点A按顺时针方向旋转到$\triangle AB_{1}C_{1}$的位置,点$B_{1}$恰好落在边BC的中点处,
$\therefore AB_{1}=\frac{1}{2}BC$,$BB_{1}=B_{1}C$,$AB=AB_{1}$,$\therefore BB_{1}=AB=AB_{1}$,
$\therefore \triangle ABB_{1}$是等边三角形,$\therefore \angle BAB_{1}=\angle B=60^{\circ}$.$\therefore \angle CAC_{1}=60^{\circ}$,
∵将$\triangle ABC$绕点A按顺时针方向旋转至$\triangle AB_{1}C_{1}$的位置,
$\therefore CA=C_{1}A$,$\therefore \triangle AC_{1}C$是等边三角形,$\therefore CC_{1}=CA$.
∵$AB=2$,$BC=4$,$\therefore CA=2\sqrt{3}$,$\therefore CC_{1}=2\sqrt{3}$.
∵在$\triangle ABC$中,$\angle BAC=90^{\circ}$,将$\triangle ABC$绕点A按顺时针方向旋转到$\triangle AB_{1}C_{1}$的位置,点$B_{1}$恰好落在边BC的中点处,
$\therefore AB_{1}=\frac{1}{2}BC$,$BB_{1}=B_{1}C$,$AB=AB_{1}$,$\therefore BB_{1}=AB=AB_{1}$,
$\therefore \triangle ABB_{1}$是等边三角形,$\therefore \angle BAB_{1}=\angle B=60^{\circ}$.$\therefore \angle CAC_{1}=60^{\circ}$,
∵将$\triangle ABC$绕点A按顺时针方向旋转至$\triangle AB_{1}C_{1}$的位置,
$\therefore CA=C_{1}A$,$\therefore \triangle AC_{1}C$是等边三角形,$\therefore CC_{1}=CA$.
∵$AB=2$,$BC=4$,$\therefore CA=2\sqrt{3}$,$\therefore CC_{1}=2\sqrt{3}$.
14. (8 分)已知六边形 $ ABCDEF $ 是以 $ O $ 为中心的中心对称图形(如图),画出六边形 $ ABCDEF $ 的全部图形,并指出所有的对应点和对应线段.
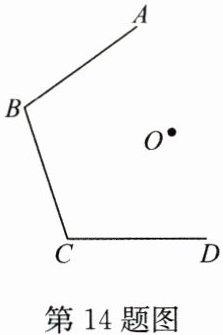

答案:
解:如图.图中点A的对应点是点D,点B的对应点是点E,点C的对应点是点F;AB的对应线段是DE,BC的对应线段是EF,CD的对应线段是AF.

解:如图.图中点A的对应点是点D,点B的对应点是点E,点C的对应点是点F;AB的对应线段是DE,BC的对应线段是EF,CD的对应线段是AF.

查看更多完整答案,请扫码查看


