《2025年提分教练九年级数学上册人教版》

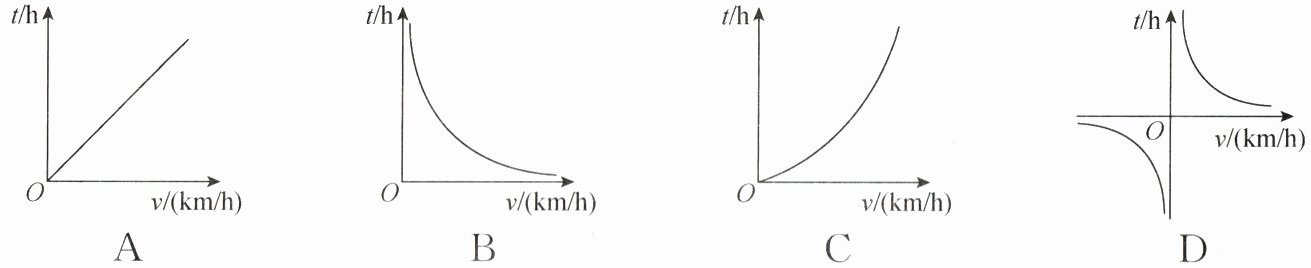
1. 已知甲,乙两地相距 $ s $(单位: $ km $),汽车从甲地匀速行驶到乙地,则汽车行驶的时间 $ t $(单位: $ h $)关于行驶速度 $ v $(单位: $ km/h $)的函数图象是(B)

答案： B

2. 若函数 $ y = \frac{k}{x}(k \neq 0) $的图象过点 $ (\sqrt{2},3) $,则关于其图象,下列叙述正确的是(B)
A.当 $ x \neq 0 $时, $ y $随 $ x $的增大而增大
B.分别在第一、三象限内, $ y $随 $ x $的增大而减小
C.当 $ x \neq 0 $时, $ y $随 $ x $的增大而减小
D.分别在第二、四象限内, $ y $随 $ x $的增大而增大

答案： B

3. 已知点 $ A(-3,y_1) $、$ B(-2,y_2) $、$ C(3,y_3) $都在反比例函数 $ y = \frac{4}{x} $的图象上,则(D)
A.$ y_1 ＜ y_2 ＜ y_3 $
B.$ y_3 ＜ y_2 ＜ y_1 $
C.$ y_3 ＜ y_1 ＜ y_2 $
D.$ y_2 ＜ y_1 ＜ y_3 $

答案： 3.D　解析:
∵点A(−3,y₁)、B(−2,y₂)、C(3,y₃)都在反比例函数y=$\frac{4}{x}$的图象上,
∴y₁=−$\frac{4}{3}$,y₂=−2,y₃=$\frac{4}{3}$.
∵−2＜−$\frac{4}{3}$＜$\frac{4}{3}$,
∴y₂＜y₁＜y₃.

4. 如图, $ \triangle ABC \backsim \triangle CBD $, $ CD = 2 $, $ AC = 3 $, $ BC = 4 $,那么 $ AB $等于(6)

A.5
B.6
C.7
D.4

答案： 4.B　解析:
∵△ABC∽△CBD,
∴$\frac{AB}{CB}$=$\frac{AC}{CD}$，即$\frac{AB}{4}$=$\frac{3}{2}$.解得AB=6.

5. 如图,小明用自制的直角三角形纸板 $ DEF $测量树 $ AB $的高度,测量时,使直角边 $ DF $始终保持水平状态,其延长线交 $ AB $于点 $ G $,使斜边 $ DE $所在的直线经过点 $ A $.测得边 $ DF $离地面的高度为 $ 1 m $,点 $ D $到 $ AB $的距离为 $ 7.5 m $.已知 $ DF = 1.5 m $, $ EF = 0.6 m $,则树 $ AB $的高度为( )

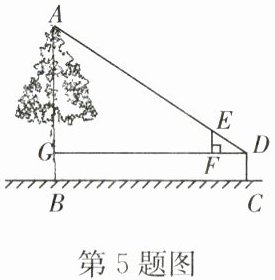
A.$ 4 m $
B.$ 4.5 m $
C.$ 4.6 m $
D.$ 4.8 m $

答案：
5.A　解析:由题意，知BG=DC=1m,DG =7.5m.
∵EF//AG,
∴△DEF∽△DAG,
∴$\frac{EF}{AG}$=$\frac{DF}{DG}$,即$\frac{0.6}{AG}$=$\frac{1.5}{7.5}$,
∴AG =3m.
∴AB=BG+AG=1+3=4(m).