《2025年提分教练九年级数学上册人教版》

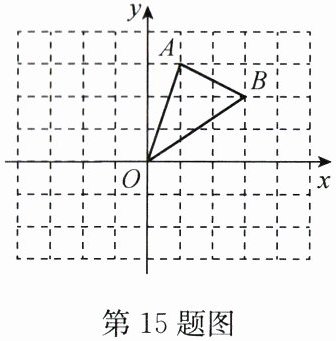
15. (10 分)如图,在边长为 1 的小正方形网格中,$ \triangle AOB $ 的顶点均在格点上。
(1) 点 $ B $ 关于 $ y $ 轴的对称点的坐标为______；
(2) 将 $ \triangle AOB $ 向左平移 3 个单位长度得到 $ \triangle A_1O_1B_1 $,请画出 $ \triangle A_1O_1B_1 $；
(3) 以原点 $ O $ 为对称中心,画出与 $ \triangle AOB $ 关于原点对称的 $ \triangle A_2OB_2 $；
(4) 以原点 $ O $ 为旋转中心,画出将 $ \triangle AOB $ 顺时针旋转 $ 90° $ 后得到的 $ \triangle A_3OB_3 $。

答案：

(1)$(-3,2)$
(2)如图,$\triangle A_{1}O_{1}B_{1}$为所求作的图形.
(3)如图,$\triangle A_{2}OB_{2}$为所求作的图形.
(4)如图,$\triangle A_{3}OB_{3}$为所求作的图形.

16. (10 分)已知关于 $ x $ 的一元二次方程 $ mx^2 + nx - 2 = 0 $。
(1) 当 $ n = m - 2 $ 时,利用根的判别式判断方程根的情况；
(2) 若方程有两个不相等的实数根,写出一组满足条件的 $ m $,$ n $ 的值,并求出此时方程的根。

答案： 1. （1）
对于一元二次方程$mx^{2}+nx - 2 = 0$（$m\neq0$），其判别式$\Delta=n^{2}+8m$。
当$n = m - 2$时，将$n=m - 2$代入$\Delta$得：
$\Delta=(m - 2)^{2}+8m$。
展开$(m - 2)^{2}+8m$：
根据完全平方公式$(a - b)^{2}=a^{2}-2ab + b^{2}$，这里$a = m$，$b = 2$，则$(m - 2)^{2}+8m=m^{2}-4m + 4+8m$。
合并同类项得$\Delta=m^{2}+4m + 4$。
再根据完全平方公式$a^{2}+2ab + b^{2}=(a + b)^{2}$，这里$a = m$，$b = 2$，所以$\Delta=(m + 2)^{2}$。
因为$(m + 2)^{2}\geqslant0$（当且仅当$m=-2$时取等号），且$m\neq0$：
当$m=-2$时，$\Delta = 0$，方程有两个相等的实数根；
当$m\neq - 2$且$m\neq0$时，$\Delta=(m + 2)^{2}\gt0$，方程有两个不相等的实数根。
2. （2）
因为方程$mx^{2}+nx - 2 = 0$有两个不相等的实数根，所以$\Delta=n^{2}+8m\gt0$，且$m\neq0$。
取$m = 2$，$n = 2$（答案不唯一），此时方程为$2x^{2}+2x - 2 = 0$。
化简方程：
方程两边同时除以$2$得$x^{2}+x - 1 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，其求根公式为$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，在方程$x^{2}+x - 1 = 0$中，$a = 1$，$b = 1$，$c=-1$。
先计算判别式$\Delta=b^{2}-4ac=1^{2}-4×1×(-1)=1 + 4 = 5$。
再代入求根公式得$x=\frac{-1\pm\sqrt{5}}{2×1}$。
所以$x_{1}=\frac{-1+\sqrt{5}}{2}$，$x_{2}=\frac{-1-\sqrt{5}}{2}$。
综上，（1）当$m=-2$时，方程有两个相等的实数根；当$m\neq - 2$且$m\neq0$时，方程有两个不相等的实数根；（2）取$m = 2$，$n = 2$时，$x_{1}=\frac{-1+\sqrt{5}}{2}$，$x_{2}=\frac{-1-\sqrt{5}}{2}$（$m$，$n$取值不唯一）。

17. (10 分)某商场经营某种儿童益智玩具。已知成批购进时每件的价格是 20 元。调查发现：当销售价格是每件 30 元时,月销售量是 230 件,而销售单价每上涨 1 元,月销售量就减少 10 件,但每件玩具的售价不能高于 40 元。求每件玩具的售价定为多少元时,月销售的利润恰为 2520 元。

答案： 设每件玩具上涨x元,则每件的售价为$(30 + x)$元.根据题意,得$(30 + x - 20)(230 - 10x)=2520$,整理,得$x^{2}-13x + 22 = 0$,解得$x_{1}=11$,$x_{2}=2$.当$x = 11$时,$30 + x = 41＞40$,
∴$x = 11$不符合题意,舍去.
∴每件玩具的售价为$30 + 2 = 32$(元).答:每件玩具的售价定为32元时,月销售的利润恰为2520元.

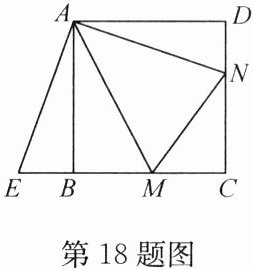
18. (10 分)如图,点 $ M $,$ N $ 分别在正方形 $ ABCD $ 的边 $ BC $,$ CD $ 上,且 $ \angle MAN = 45° $。把 $ \triangle ADN $ 绕点 $ A $ 顺时针旋转 $ 90° $ 得到 $ \triangle ABE $。
(1) 求证：$ \triangle AEM \cong \triangle ANM $。
(2) 若 $ BM = 3 $,$ DN = 2 $,求正方形 $ ABCD $ 的边长。

答案：
(1)证明:由旋转的性质得,$\triangle ADN\cong\triangle ABE$,
∴$∠DAN = ∠BAE$,$AE = AN$;
∵$∠DAB = 90^{\circ}$,$∠MAN = 45^{\circ}$,
∴$∠MAE = ∠BAE + ∠BAM = ∠DAN + ∠BAM = 45^{\circ}$,
∴$∠MAE = ∠MAN$.
∵$MA = MA$,
∴$\triangle AEM\cong\triangle ANM(SAS)$.
(2)解:设$CD = BC = x$,则$CM = x - 3$,$CN = x - 2$,
∵$\triangle AEM\cong\triangle ANM$,
∴$EM = MN$.
∵$BE = DN$,
∴$MN = BM + DN = 5$.
∵$∠C = 90^{\circ}$,
∴$MN^{2}=CM^{2}+CN^{2}$,
∴$25=(x - 3)^{2}+(x - 2)^{2}$,解得$x = 6$或$x = -1$(舍),
∴正方形ABCD的边长为6.