第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
19. (12 分)某商场出售一批进价为 2 元的贺卡,在市场营销中发现,这种商品的日销售单价 x(元)与日销售量 y(个)之间的关系如下:

(1)根据表中数据在平面直角坐标系中描出实数对 $ (x,y) $ 的对应点。
(2)猜测并确定 y 与 x 之间的函数关系式。
(3)设销售这种贺卡的销售利润为 w 元,若物价局规定这种贺卡的售价不能超过 10 元/个,则当日销售单价定为多少元时,才能获得最大日销售利润?

(1)根据表中数据在平面直角坐标系中描出实数对 $ (x,y) $ 的对应点。
(2)猜测并确定 y 与 x 之间的函数关系式。
(3)设销售这种贺卡的销售利润为 w 元,若物价局规定这种贺卡的售价不能超过 10 元/个,则当日销售单价定为多少元时,才能获得最大日销售利润?
答案:
(1)描点如图。
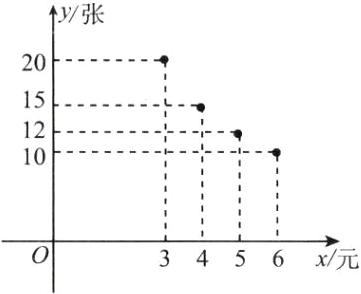
(2)根据图象猜测,y与x成反比例函数关系。设$y=\frac{k}{x}(k≠0)$,把点$(3,20)$的坐标代入$y=\frac{k}{x}$,得$k=60$。
∴$y=\frac{60}{x}(x≥2)$。把点$(4,15)$,$(5,12)$,$(6,10)$的坐标代入上式均成立。
∴y与x之间的函数关系式为$y=\frac{60}{x}(x≥2)$。
(3)由
(2)及已知得,$w=(x−2)\cdot y=(x−2)\cdot \frac{60}{x}=60-\frac{120}{x}$ $(2≤x≤10)$。当$x=10$时,w取得最大值。故当日销售单价定为10元时,才能获得最大日销售利润。
(1)描点如图。

(2)根据图象猜测,y与x成反比例函数关系。设$y=\frac{k}{x}(k≠0)$,把点$(3,20)$的坐标代入$y=\frac{k}{x}$,得$k=60$。
∴$y=\frac{60}{x}(x≥2)$。把点$(4,15)$,$(5,12)$,$(6,10)$的坐标代入上式均成立。
∴y与x之间的函数关系式为$y=\frac{60}{x}(x≥2)$。
(3)由
(2)及已知得,$w=(x−2)\cdot y=(x−2)\cdot \frac{60}{x}=60-\frac{120}{x}$ $(2≤x≤10)$。当$x=10$时,w取得最大值。故当日销售单价定为10元时,才能获得最大日销售利润。
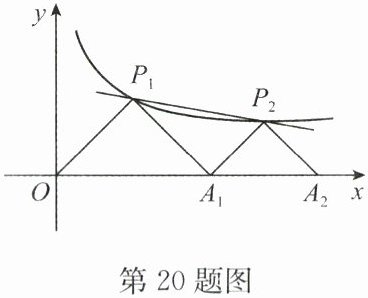
20. (12 分)如图,$ P_1 $、$ P_2 $ 是反比例函数 $ y = \frac{k}{x}(k > 0) $ 在第一象限的图象上的两点,点 $ A_1 $ 的坐标为 $ (4,0) $。若 $ \triangle P_1OA_1 $ 与 $ \triangle P_2A_1A_2 $ 均为等腰直角三角形,其中点 $ P_1 $、$ P_2 $ 为直角顶点。
(1)求反比例函数的解析式。
(2)①求点 $ P_2 $ 的坐标。
②根据图象直接写出在第一象限内,当 x 满足什么条件时,图象经过点 $ P_1 $、$ P_2 $ 的一次函数的函数值大于反比例函数 $ y = \frac{k}{x} $ 的函数值。
(1)求反比例函数的解析式。
(2)①求点 $ P_2 $ 的坐标。
②根据图象直接写出在第一象限内,当 x 满足什么条件时,图象经过点 $ P_1 $、$ P_2 $ 的一次函数的函数值大于反比例函数 $ y = \frac{k}{x} $ 的函数值。

答案:
(1)过点$P_{1}$作$P_{1}B⊥x$轴,垂足为B。
∵点$A_{1}$的坐标为$(4,0)$,$△P_{1}OA_{1}$为等腰直角三角形,
∴$OB=2$,$P_{1}B=\frac{1}{2}OA_{1}=2$,
∴$P_{1}$的坐标为$(2,2)$。将$P_{1}$的坐标代入$y=\frac{k}{x}(k>0)$,得$k=2×2=4$,
∴反比例函数的解析式为$y=\frac{4}{x}$。
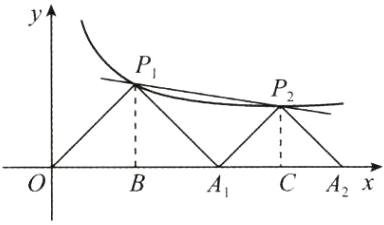
(2)①过点$P_{2}$作$P_{2}C⊥x$轴,垂足为C。
∵$△P_{2}A_{1}A_{2}$为等腰直角三角形,
∴$P_{2}C=A_{1}C$。设$P_{2}C=A_{1}C=a$,则$P_{2}$的坐标为$(4+a,a)$,将$P_{2}$的坐标代入反比例函数的解析式$y=\frac{4}{x}$,得$a=\frac{4}{4+a}$,解得$a=2\sqrt{2}-2$或$a=-2\sqrt{2}-2$(舍去)。
∴点$P_{2}$的坐标为$(2+2\sqrt{2},2\sqrt{2}-2)$。
②在第一象限内,当$2<x<2+2\sqrt{2}$时,一次函数的函数值大于反比例函数的函数值。
(1)过点$P_{1}$作$P_{1}B⊥x$轴,垂足为B。
∵点$A_{1}$的坐标为$(4,0)$,$△P_{1}OA_{1}$为等腰直角三角形,
∴$OB=2$,$P_{1}B=\frac{1}{2}OA_{1}=2$,
∴$P_{1}$的坐标为$(2,2)$。将$P_{1}$的坐标代入$y=\frac{k}{x}(k>0)$,得$k=2×2=4$,
∴反比例函数的解析式为$y=\frac{4}{x}$。

(2)①过点$P_{2}$作$P_{2}C⊥x$轴,垂足为C。
∵$△P_{2}A_{1}A_{2}$为等腰直角三角形,
∴$P_{2}C=A_{1}C$。设$P_{2}C=A_{1}C=a$,则$P_{2}$的坐标为$(4+a,a)$,将$P_{2}$的坐标代入反比例函数的解析式$y=\frac{4}{x}$,得$a=\frac{4}{4+a}$,解得$a=2\sqrt{2}-2$或$a=-2\sqrt{2}-2$(舍去)。
∴点$P_{2}$的坐标为$(2+2\sqrt{2},2\sqrt{2}-2)$。
②在第一象限内,当$2<x<2+2\sqrt{2}$时,一次函数的函数值大于反比例函数的函数值。
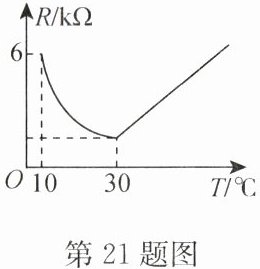
21. (13 分)家用电灭蚊器的发热部分使用了 PTC 发热材料,它的电阻 $ R(k\Omega) $ 随温度 $ T(^{\circ}C) $(在一定范围内)变化的大致图象如图所示。通电后,发热材料的温度在由室温 $ 10^{\circ}C $ 上升到 $ 30^{\circ}C $ 的过程中,电阻与温度成反比例关系,且在温度达到 $ 30^{\circ}C $ 时,电阻下降到最小值;随后电阻随温度的升高而增大,温度每上升 $ 1^{\circ}C $,电阻增加 $ \frac{4}{15}k\Omega $。
(1)求 R 和 T 之间的解析式。
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过 $ 4k\Omega $?
(1)求 R 和 T 之间的解析式。
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过 $ 4k\Omega $?

答案:
(1)
∵温度在由室温$10^{\circ}C$上升到$30^{\circ}C$的过程中,电阻与温度成反比例关系,
∴当$10≤T≤30$时,设解析式为$R=\frac{k}{T}$。将$(10,6)$代入上式,得$6=\frac{k}{10}$,
∴$k=6×10=60$,
∴$R=\frac{60}{T}$。将$T=30$代入上式,得$R=2$。
∴温度为$30^{\circ}C$时,电阻R的最小值为2kΩ。
∵随后电阻随温度的升高而增大,温度每上升$1^{\circ}C$,电阻增大$\frac{4}{15}kΩ$,
∴当$T>30$时,$R=2+\frac{4}{15}(T−30)=\frac{4}{15}T−6$。故R和T之间的解析式为$R=\begin{cases}\frac{60}{T}(10\leq T\leq30)\frac{4}{15}T−6(T>30)\end{cases}$。
(2)把$R=4$代入$R=\frac{4}{15}T−6$,得$T=37.5$,把$R=4$代入$R=\frac{60}{T}$,得$T=15$,
∴温度在$15^{\circ}C\sim37.5^{\circ}C$时,发热材料的电阻不超过4kΩ。
(1)
∵温度在由室温$10^{\circ}C$上升到$30^{\circ}C$的过程中,电阻与温度成反比例关系,
∴当$10≤T≤30$时,设解析式为$R=\frac{k}{T}$。将$(10,6)$代入上式,得$6=\frac{k}{10}$,
∴$k=6×10=60$,
∴$R=\frac{60}{T}$。将$T=30$代入上式,得$R=2$。
∴温度为$30^{\circ}C$时,电阻R的最小值为2kΩ。
∵随后电阻随温度的升高而增大,温度每上升$1^{\circ}C$,电阻增大$\frac{4}{15}kΩ$,
∴当$T>30$时,$R=2+\frac{4}{15}(T−30)=\frac{4}{15}T−6$。故R和T之间的解析式为$R=\begin{cases}\frac{60}{T}(10\leq T\leq30)\frac{4}{15}T−6(T>30)\end{cases}$。
(2)把$R=4$代入$R=\frac{4}{15}T−6$,得$T=37.5$,把$R=4$代入$R=\frac{60}{T}$,得$T=15$,
∴温度在$15^{\circ}C\sim37.5^{\circ}C$时,发热材料的电阻不超过4kΩ。
查看更多完整答案,请扫码查看


