《2025年提分教练九年级数学上册人教版》

19. (11 分)已知关于 $ x $ 的一元二次方程 $ x ^ { 2 } - ( k + 5 ) x + 3 k + 6 = 0 $。
(1)求证：此方程总有两个实数根；
(2)若此方程有一个根大于 - 2 且小于 0,$ k $ 为整数,求 $ k $ 的值。

答案：
(1)证明:依题意，得$\Delta=[-(k+5)]^2-4(3k+6)=k^2-2k+1=(k-1)^2$.
∵$(k-1)^2\geqslant0$，
∴此方程总有两个实数根.
(2)解:解方程得$x=\frac{(k+5)\pm\sqrt{(k-1)^2}}{2}$，
∴方程的两个根为$x_1=k+2$，$x_2=3$.
　由题意可知，$-2＜k+2＜0$，即$-4＜k＜-2$.
∵$k$为整数，
∴$k=-3$.

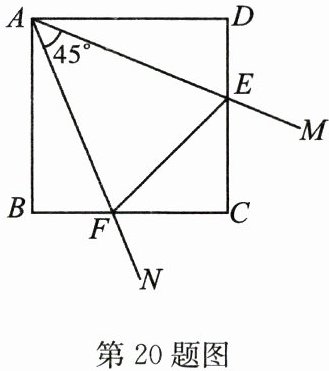
20. (11 分)如图,过正方形 $ ABCD $ 的顶点 $ A $ 作射线 $ AM $ 交 $ DC $ 于点 $ E $,将 $ AM $ 绕点 $ A $ 顺时针旋转 $ 45 ^ { \circ } $ 到射线 $ AN $ 的位置,$ AN $ 交 $ BC $ 于点 $ F $,连接 $ EF $。
(1)试猜想三条线段 $ BF $,$ DE $,$ EF $ 之间的数量关系；
(2)请证明你的猜想。

答案：

(1)$EF=BF+DE$；
(2)证明:
∵四边形$ABCD$是正方形，
∴$AD=AB$，$\angle D=\angle ABC=\angle BAD=90°$.
　如图，将$\triangle ADE$绕点$A$旋转到$AD$和$AB$重合，得$\triangle ABG$，
　　　　　　　　　　　　　　
∴$\triangle ADE\cong\triangle ABG$，
∴$AE=AG$，$DE=BG$，$\angle DAE=\angle BAG$，$\angle D=\angle ABG=\angle ABC$，
∴$G$，$B$，$F$三点在一条直线上.
∵$\angle BAF+\angle DAE=\angle BAD-\angle EAF=90°-45°=45°$，
∴$\angle GAB+\angle BAF=45°$.
　即$\angle GAF=45°$.
∴$\angle GAF=\angle EAF$；
　在$\triangle GAF$和$\triangle EAF$中，$\begin{cases}AG=AE\\\angle GAF=\angle EAF\\AF=AF\end{cases}$
∴$\triangle GAF\cong\triangle EAF$，
∴$GB+BF=EF$.
∴$DE+BF=EF$；

21. (13 分)某公司去年年初投资 1 200 万元购买新生产线生产新产品,此外,生产每件该产品还需要成本 60 元,按规定,该产品售价不得低于 80 元/件且不超过 160 元/件,该产品的年销售量 $ y $(万件)与产品售价 $ x $(元/件)之间的关系如图所示。
(1)求 $ y $ 与 $ x $ 的函数关系式,并写出 $ x $ 的取值范围。
(2)求该公司去年所获利润的最大值。
(3)在去年获利最大的前提下,公司今年重新确定产品的售价,能否使去年和今年共获利 1 000 万元？若能,请求出今年的产品售价；若不能,请说明理由。

答案：
(1)设$y=kx+b$，则$\begin{cases}80k+b=22\\160k+b=14\end{cases}$，解得$\begin{cases}k=-\frac{1}{10}\\b=30\end{cases}$
∴$y$与$x$的函数关系式为$y=-\frac{1}{10}x+30(80\leqslant x\leqslant160)$.
(2)设公司去年获利$w$万元，
　则$w=(x-60)\left(-\frac{1}{10}x+30\right)-1200=-\frac{1}{10}(x-180)^2+240$.
∵$-\frac{1}{10}＜0$，$80\leqslant x\leqslant160$，
∴当$x=160$时，$w$取得最大值200.
∴去年所获利润的最大值为200万元.
(3)根据题意，得$(x-60)\left(-\frac{1}{10}x+30\right)+200=1000$，
　解得$x_1=100$，$x_2=260$.
∵$80\leqslant x\leqslant160$，
∴$x=100$.
　答:今年的产品售价定为100元/件时，可使去年和今年共获利1000万元.