第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
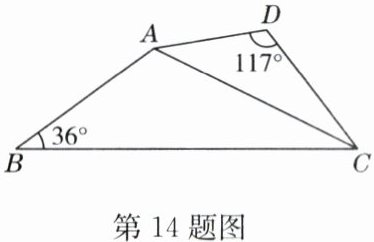
14. (10 分)如图,已知$AD = 3cm$,$AC = 6cm$,$BC = 9cm$,$\angle B = 36^{\circ}$,$\angle D = 117^{\circ}$,$\triangle ABC \sim \triangle DAC$.
(1)求$AB$的长;
(2)求$\angle BAD$的大小.
(1)求$AB$的长;
(2)求$\angle BAD$的大小.

答案:
解:
(1)
∵△ABC∽△DAC,
∴$\frac{AB}{AD}=\frac{BC}{AC}$.又
∵AD = 3cm,AC = 6cm,BC = 9cm,
∴AB = 4.5cm.
(2)
∵△ABC∽△DAC,
∴∠DAC = ∠B = 36°,∠BAC = ∠D = 117°,
∴∠BAD = ∠DAC + ∠BAC = 36° + 117° = 153°.
(1)
∵△ABC∽△DAC,
∴$\frac{AB}{AD}=\frac{BC}{AC}$.又
∵AD = 3cm,AC = 6cm,BC = 9cm,
∴AB = 4.5cm.
(2)
∵△ABC∽△DAC,
∴∠DAC = ∠B = 36°,∠BAC = ∠D = 117°,
∴∠BAD = ∠DAC + ∠BAC = 36° + 117° = 153°.
15. (10 分)如图,在等边三角形$ABC$中,点$D$,$E分别在BC$,$AB$上,且$\angle ADE = 60^{\circ}$.
求证:$\triangle ADC \sim \triangle DEB$.

求证:$\triangle ADC \sim \triangle DEB$.

答案:
证明:
∵△ABC是等边三角形,
∴∠B = ∠C = 60°,
∴∠ADB = ∠CAD + ∠C = ∠CAD + 60°.
∵∠ADE = 60°,
∴∠ADB = ∠BDE + 60°,
∴∠CAD = ∠BDE,
∴△ADC∽△DEB.
∵△ABC是等边三角形,
∴∠B = ∠C = 60°,
∴∠ADB = ∠CAD + ∠C = ∠CAD + 60°.
∵∠ADE = 60°,
∴∠ADB = ∠BDE + 60°,
∴∠CAD = ∠BDE,
∴△ADC∽△DEB.
16. (12 分)如图,将$\triangle ABC$在网格中(网格中每个小正方形的边长均为 1)依次进行位似变换、轴对称变换和平移变换后得到$\triangle A_3B_3C_3$.
(1)$\triangle ABC与\triangle A_1B_1C_1$的相似比等于______.
(2)在网格中画出$\triangle A_1B_1C_1关于y轴的轴对称图形\triangle A_2B_2C_2$.
(3)请写出$\triangle A_3B_3C_3是由\triangle A_2B_2C_2$怎样平移得到的.
(4)设点$P(x,y)为\triangle ABC$内一点,依次经过上述三次变换后,点$P$的对应点的坐标为______.

(1)$\triangle ABC与\triangle A_1B_1C_1$的相似比等于______.
(2)在网格中画出$\triangle A_1B_1C_1关于y轴的轴对称图形\triangle A_2B_2C_2$.
(3)请写出$\triangle A_3B_3C_3是由\triangle A_2B_2C_2$怎样平移得到的.
(4)设点$P(x,y)为\triangle ABC$内一点,依次经过上述三次变换后,点$P$的对应点的坐标为______.

答案:
解:
(1)$\frac{1}{2}$
(2)如图所示.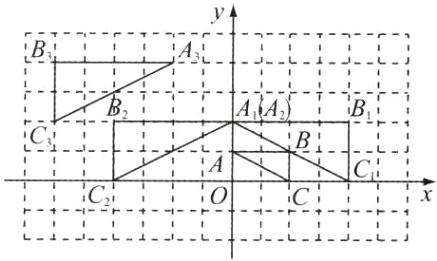
(3)△A₃B₃C₃是由△A₂B₂C₂沿x轴向左平移2个单位长度,再沿y轴向上平移2个单位长度得到的.
(4)(−2x−2,2y+2)
解:
(1)$\frac{1}{2}$
(2)如图所示.

(3)△A₃B₃C₃是由△A₂B₂C₂沿x轴向左平移2个单位长度,再沿y轴向上平移2个单位长度得到的.
(4)(−2x−2,2y+2)
17. (12 分)已知两个直角三角形的三边长分别为 3,4,$m$和 6,8,$n$,且这两个直角三角形不相似,求$m + n$的值.
答案:
解:在第一个直角三角形中,若m是直角边,则$m = \sqrt{4^{2}-3^{2}}=\sqrt{7}$;若m是斜边,则$m = \sqrt{4^{2}+3^{2}}=5$.在第二个直角三角形中,若n是直角边,则$n = \sqrt{8^{2}-6^{2}}=\sqrt{28}=2\sqrt{7}$;若n是斜边,则$n = \sqrt{8^{2}+6^{2}}=10$.又因为两个直角三角形不相似,所以$m = 5,n = 2\sqrt{7}$或$m = \sqrt{7},n = 10$,当$m = 5,n = 2\sqrt{7}$时,$m + n = 5 + 2\sqrt{7}$,当$m = \sqrt{7},n = 10$时,$m + n = 10 + \sqrt{7}$.
查看更多完整答案,请扫码查看


