第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
7. 如图,$AB是\odot O$的弦,$AC是\odot O$的切线,$A$为切点,$BC$经过圆心,若$\angle OBA = 25^{\circ}$,则$\angle BCA$的度数为(
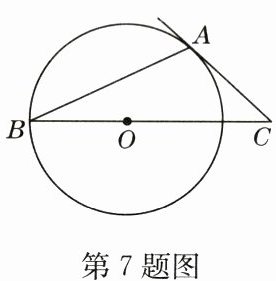
A.$20^{\circ}$
B.$25^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
C
)
A.$20^{\circ}$
B.$25^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
答案:
C 解析:连接 OA.
∵OA=OB,
∴∠OAB=∠OBA=25°,
∴∠AOC=∠OBA+∠OAB=50°,
∵AC 是⊙O 的切线,
∴∠OAC=90°,
∴∠BCA=40°.
∵OA=OB,
∴∠OAB=∠OBA=25°,
∴∠AOC=∠OBA+∠OAB=50°,
∵AC 是⊙O 的切线,
∴∠OAC=90°,
∴∠BCA=40°.
8. 如图,$PA$,$PB分别切圆O于点A$,$B$,$AC是\odot O$的直径,连接$AB$,$BC$,$OP$,则与$\angle APO$相等的角的个数是(
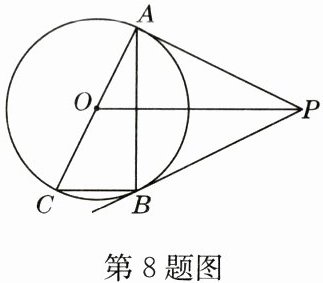
A.2
B.3
C.4
D.5
B
)
A.2
B.3
C.4
D.5
答案:
B
9. 如图,已知四边形$ABCD是\odot O$的内接四边形,$\angle B = 140^{\circ}$,则$\angle AOC = $
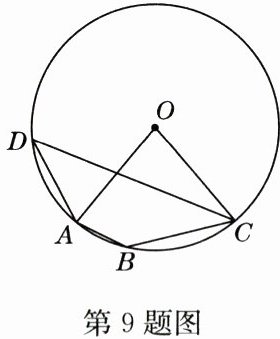
80°
.
答案:
80° 解析:
∵四边形 ABCD 是⊙O 的内接四边形,∠B=140°,
∴∠D=180°-∠B=40°,
∴∠AOC=2∠D=80°.
∵四边形 ABCD 是⊙O 的内接四边形,∠B=140°,
∴∠D=180°-∠B=40°,
∴∠AOC=2∠D=80°.
10. 如图,$AB$、$AC$、$BD都是\odot O$的切线,$P$、$C$、$D$为切点,如果$AB = 5$,$AC = 3$,那么$BD$的长为______.
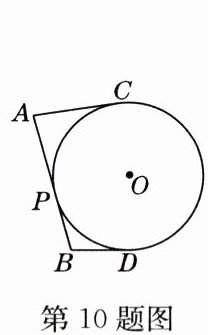

2
答案:
2
11. 已知三角形的三边长分别为 3 cm、4 cm、5 cm,则这个三角形外接圆的半径是
2.5 cm
.
答案:
2.5 cm
12. 如果一个扇形的弧长等于它的半径,那么此扇形被称为等边扇形,那么半径为 2 的等边扇形的面积为
2
.
答案:
2
13. 如图,$MN$是半径为 1 的$\odot O$的直径,点$A在\odot O$上,$\angle AMN = 30^{\circ}$,$B为\overset{\frown}{AN}$的中点,$P是直径MN$上一动点,则$PA + PB$的最小值为______.
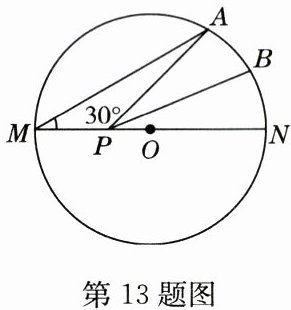

答案:
$\sqrt{2}$ 解析:作点 B 关于直线 MN 的对称点为 B',连接 OA、OB、OB'、AB',如图,则 AB'与 MN 的交点即为 PA+PB 的值最小时的点P,且 PA+PB 的最小值=AB'.
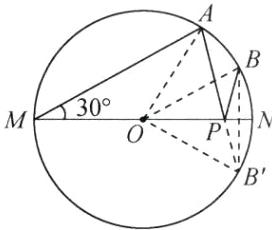
∵∠AMN=30°,OA=OM,
∴∠AON=2∠AMN=2×30°=60°,
∵点 B 为劣弧$\overset{\frown}{AN}$的中点,
∴∠BON=$\frac{1}{2}$∠AON=$\frac{1}{2}$×60°=30°,由对称性可得∠B'ON=∠BON=30°,
∴∠AOB'=∠AON+∠B'ON=60°+30°=90°,
∴△AOB'是等腰直角三角形,
∴AB'=$\sqrt{2}$OA=$\sqrt{2}$×1=$\sqrt{2}$,即 PA+PB 的最小值为$\sqrt{2}$.
$\sqrt{2}$ 解析:作点 B 关于直线 MN 的对称点为 B',连接 OA、OB、OB'、AB',如图,则 AB'与 MN 的交点即为 PA+PB 的值最小时的点P,且 PA+PB 的最小值=AB'.

∵∠AMN=30°,OA=OM,
∴∠AON=2∠AMN=2×30°=60°,
∵点 B 为劣弧$\overset{\frown}{AN}$的中点,
∴∠BON=$\frac{1}{2}$∠AON=$\frac{1}{2}$×60°=30°,由对称性可得∠B'ON=∠BON=30°,
∴∠AOB'=∠AON+∠B'ON=60°+30°=90°,
∴△AOB'是等腰直角三角形,
∴AB'=$\sqrt{2}$OA=$\sqrt{2}$×1=$\sqrt{2}$,即 PA+PB 的最小值为$\sqrt{2}$.
14. (9 分)如图,已知$\odot O的直径AB与弦AC的夹角为30^{\circ}$,过点$C作\odot O的切线交AB的延长线于点D$,$OD = 30$ cm,求直径$AB$的长.
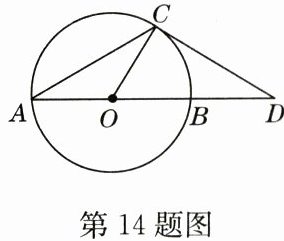

答案:
解:
∵∠A=30°,OC=OA,
∴∠ACO=∠A=30°,
∴∠COD=60°,
∵DC 切⊙O 于 C,
∴∠OCD=90°,
∴∠D=30°,
∵OD=30 cm,
∴OC=$\frac{1}{2}$OD=15 cm,
∴AB=2OC=30 cm.
∵∠A=30°,OC=OA,
∴∠ACO=∠A=30°,
∴∠COD=60°,
∵DC 切⊙O 于 C,
∴∠OCD=90°,
∴∠D=30°,
∵OD=30 cm,
∴OC=$\frac{1}{2}$OD=15 cm,
∴AB=2OC=30 cm.
查看更多完整答案,请扫码查看


