《2025年学习检测九年级数学上册华师大版河南专版》

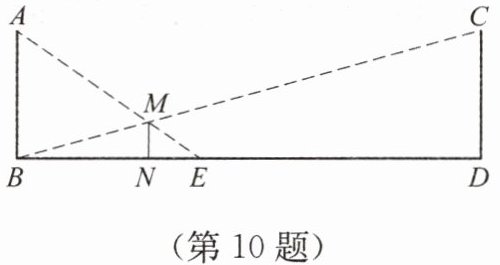
10. 如图,马路两侧有两根灯杆 AB、CD,当小明站在点 N 处时,在灯 C 的照射下,小明的影长正好为 NB 的长,在灯 A 的照射下,小明的影长为 NE 的长,测得 $BD = 24$ m,$NB = 6$ m,$NE = 2$ m.
(1) 若小明的身高 $MN = 1.6$ m,求 AB 的长;
(2) 试判断这两根灯杆的高度是否相等,并说明理由.

答案：
(1)
∵MN//AB,
∴△MNE∽△ABE.
∴$\frac{MN}{AB}=\frac{NE}{BE}$.
∵NB=6m,NE=2m,MN=1.6m,
∴$\frac{1.6}{AB}=\frac{2}{2+6}$.
∴AB=6.4m.
(2)这两根灯杆的高度相等.理由如下:由
(1)可知,$\frac{MN}{AB}=\frac{NE}{BE}=\frac{2}{8}=\frac{1}{4}$.
∵MN//CD,
∴△BNM∽△BDC.
∴$\frac{MN}{CD}=\frac{BN}{BD}=\frac{6}{24}=\frac{1}{4}$.
∴$\frac{MN}{AB}=\frac{MN}{CD}$.
∴AB=CD.

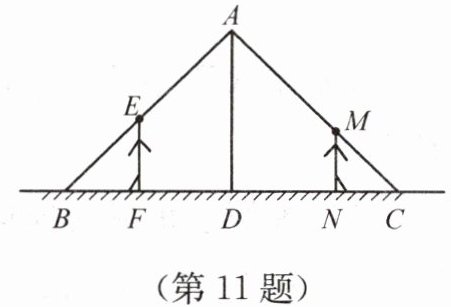
11. 贝贝利用所学知识测量路灯的高度. 如图,贝贝和爸爸站在路灯下,爸爸的身高 $EF = 1.75$ m,贝贝的身高 $MN = 1.55$ m,他们的影子恰巧等于自己的身高,即 $BF = 1.75$ m,$CN = 1.55$ m,两人之间的距离 $FN = 5.7$ m,求路灯 AD 的高度.

答案：
∵EF//AD,
∴△EBF∽△ABD.
∴$\frac{BF}{BD}=\frac{EF}{AD}$.
∵BF=EF=1.75m,
∴$\frac{1.75}{1.75+DF}=\frac{1.75}{AD}$.
∴1.75+DF=AD.同理可得,$\frac{MN}{AD}=\frac{CN}{CD}$.
∵MN=CN=1.55m,
∴$\frac{1.55}{AD}=\frac{1.55}{1.55+DN}$.
∴1.55+DN=AD.
∴1.75+DF+1.55+DN=2AD,即1.75+1.55+FN=2AD.又
∵FN=5.7m,
∴AD=4.5m.

1. 在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ \angle B = 2 \angle A $,则 $ AB : BC $ 等于【B】
A.$ 1 : 2 $
B.$ 2 : 1 $
C.$ 1 : 1 $
D.$ 1 : 3 $

答案： B.

2. 在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ c = 10 $,$ a : b = 3 : 4 $,则 $ a $ 为【C】
A.$ 3 $
B.$ 4 $
C.$ 6 $
D.$ 8 $

答案： C.

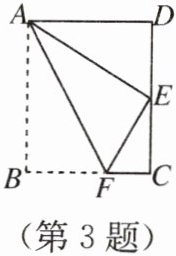
3. 如图,四边形 $ ABCD $ 为矩形纸片,把纸片 $ ABCD $ 折叠,使点 $ B $ 恰好落在 $ CD $ 边的中点 $ E $ 处,折痕为 $ AF $,若 $ CD = 6 $,则 $ AD $ 等于【B】

A.$ 4 \sqrt{3} $
B.$ 3 \sqrt{3} $
C.$ 4 \sqrt{2} $
D.$ 8 $

答案： B.